Keskiluvut

Lukuaika noin 6 min
SPSS-harjoitukset

Yhden muuttujan analyysissa mielenkiinto useimmiten kohdistuu muuttujan jakaumaan eli siihen, miten ja mille vaihteluvälille muuttujan arvot ovat jakautuneet. Yksi tapa tarkastella jakaumaa on käyttää graafisia kuvioita. Joskus on tarpeellista tiivistää jakaumaa kuvaava informaatio yhden tai useamman tunnusluvun avulla. Tällöin voidaan käyttää ns. keski- ja hajontalukuja. Keskiluvut kuvaavat muuttujien arvojen keskimääräistä suuruutta ja hajontaluvut sitä, kuinka paljon muuttujan arvot vaihtelevat.

Soveltuvan keskiluvun valintaan vaikuttaa muuttujan mittaustaso. Taulukossa 1 on esitetty sopivat keskiluvut tarkastelun kohteena olevan muuttujan mittaustason mukaan.


Taulukko 1. Soveltuvan keskiluvun valinta muuttujan mittaustason mukaan.
X = voi käyttää
- = ei voi käyttää
Muuttujan mittaustaso
Luokittelu- asteikko Järjestys- asteikko Välimatka- asteikko Suhde- asteikko
Keskiluku Moodi X X X X
Mediaani - X X X
Aritmeettinen keskiarvo - - X X
Geometrinen ja harmoninen keskiarvo - - - X

Taulukossa 2 on esitetty kuvitteellinen esimerkkiaineisto työpaikan työntekijöistä ja kolmesta heiltä mitatusta muuttujasta. Sukupuolimuuttuja on mitattu luokitteluasteikolla, koska siinä on kaksi vaihtoehtoa, joita ei voi asettaa suuruusjärjestykseen. Koulutusmuuttuja on järjestysasteikon muuttuja. Siinä on kolme vaihtoehtoa, jotka voidaan järjestää koulutuksen laajuuden mukaan. Lasten lukumäärä on suhdeasteikolla mitattu muuttuja. Taulukon muuttujien tietoja voidaan tiivistää tunnusluvuiksi käyttämällä soveltuvia keskilukuja.

Taulukko 2. Kuvitteellinen aineisto työpaikan kymmenestä työntekijästä.
Työntekijän havaintonumero Sukupuoli Koulutus Lasten määrä
Työntekijä 1 Mies Peruskoulu 0
Työntekijä 2 Nainen Keskiaste 4
Työntekijä 3 Nainen Keskiaste 1
Työntekijä 4 Mies Korkeakoulu 1
Työntekijä 5 Nainen Keskiaste 2
Työntekijä 6 Nainen Korkeakoulu 1
Työntekijä 7 Nainen Korkeakoulu 1
Työntekijä 8 Mies Peruskoulu 0
Työntekijä 9 Mies Korkeakoulu 0
Työntekijä 10 Nainen Keskiaste 2

Moodi Ankkurilinkki ikoni

Moodi (mode) eli tyyppiarvo on kaikkein joustavin keskiluku siinä mielessä, että sitä voidaan käyttää kaikissa tilanteissa muuttujan mittaustasosta huolimatta. Jos muuttujan mittaustaso on luokitteluasteikko, on moodi ainoa mahdollinen keskiluku. Moodi on yksinkertaisesti se muuttujan arvo, jonka frekvenssi aineistossa on suurin.

Esimerkiksi taulukon 2 aineistossa on neljä miestä ja kuusi naista. Näin sukupuolimuuttujan moodi on "nainen". Yleisin lapsiluku on yksi, eli taulukossa esitetyn lapsilukumuuttujan moodi on 1.

Muuttujalla voi olla myös useita moodeja. Näin käy silloin kun kahden tai useamman muuttujan arvon frekvenssi ovat yhtä suuria ja samalla suurimmat koko aineistossa. Koulutuksen osalta yleisimmät arvot ovat "keskiasteen" ja "korkeakouluasteen koulutus" eli koulutusmuuttujalla on kaksi moodia.

Mediaani Ankkurilinkki ikoni

Mediaani (median) on keskiluku, jota voidaan käyttää järjestysasteikolla, välimatka- tai suhdeasteikolla mitatun muuttujan yhteydessä. Mediaani on suuruusjärjestykseen asetetuista muuttujan arvoista keskimmäinen. Jos havaintoja on parillinen määrä, riippuu mediaanin arvo siitä, onko muuttuja mitattu järjestysasteikolla vai välimatka- tai suhdeasteikolla. Jos mittaustaso on järjestysasteikko, on mediaani tässä tapauksessa kumpikin keskimmäisistä arvoista. Jos mittaustasona on välimatka- tai suhdeasteikko, on mediaani kahden keskimmäisen arvon keskiarvo.

Esimerkiksi taulukon 2 lapsien määrää koskevat havainnot voidaan asettaa suuruusjärjestykseen seuraavalla tavalla:

0 0 0 1 1 1 1 2 2 4

Koska taulukossa on parillinen määrä havaintoja, täytyy mediaanin määrittelemiseksi löytää kaksi keskimmäistä arvoa. Nämä ovat 1 ja 1. Koska muuttujan mittaustaso on suhdeasteikko, on aineiston mediaani näiden kahden havainnon keskiarvo eli 1.

Koulutusmuuttujan osalta havaintojen suuruusjärjestys on (P=peruskoulu, KE=keskiaste, KO=korkeakoulu):

P P KE KE KE KE KO KO KO KO

Mediaani on tämän muuttujan osalta "keskiasteen koulutus".

Koska sukupuolimuuttuja on luokitteluasteikon muuttuja, siitä ei voi laskea mediaania.

Mediaanin erityinen hyöty keskilukuna on, että siihen eivät vaikuta muista muuttujan arvoista huomattavasti poikkeavat suuret tai pienet arvot. Jos havaintojen määrä on pieni, voivat tällaiset äärimmäisen poikkeavat arvot vaikuttaa suuresti aritmeettisen keskiarvon suuruuteen. Tämän vuoksi esimerkiksi palkkatietoja raportoitaessa käytetään yleensä keskilukuna mediaania keskiarvon sijasta. Tällöin joidenkin henkilöiden erittäin suuret palkat eivät vaikuta "vääristävästi" tuloksiin, kun keskustellaan keskimääräisestä palkasta.

Soveltuvan keskiluvun valinta riippuu myös siitä, mitä muuttujan ominaisuutta halutaan korostaa. Joissakin tapauksissa palkkojen aritmeettinen keskiarvo voi olla parempi keskiluvun mittari kuin mediaani.

Aritmeettinen keskiarvo Ankkurilinkki ikoni

Aritmeettinen keskiarvo (mean) on kaikkein yleisin muuttujan "keskimääräisyyttä" kuvaava keskiluku. Sitä käytetään välimatka- tai suhdeasteikolla mitattuihin muuttujiin. Aritmeettinen keskiarvo saadaan laskemalla kaikki havaintojen arvot yhteen ja jakamalla saatu summa havaintojen määrällä. Eli tutun kaavan mukaan:

$$ keskiarvo = {havaintojen ​ summa \over havaintojen ​ määrä} $$

keskiarvo = havaintojen summa / havaintojen määrä

Esimerkiksi taulukon 2 lapsimäärien keskiarvo on \( (0+4+1+1+2+1+1+0+0+2)/10=1,2 \) (0+4+1+1+2+1+1+0+0+2)/10=1,2

Aritmeettinen keskiarvo on intuitiivisesti helppo ymmärtää ja siksi erittäin suosittu keskiluku. Silti kannattaa muistaa, että poikkeavat muuttujan arvot voivat vaikuttaa suuresti aritmeettisen keskiarvon suuruuteen etenkin pienissä aineistoissa. Esimerkiksi lukusarjan (1,1,1,1,100) aritmeettinen keskiarvo on 20,8 ja saman lukusarjan mediaani 1.

Geometrinen ja harmoninen keskiarvo Ankkurilinkki ikoni

Geometrinen ja harmoninen keskiarvo ovat suhdeasteikon muuttujille sopivia keskilukuja. Koska aritmeettinen keskiarvo sopii hyvin myös suhdeasteikon muuttujille, on geometrisen ja harmonisen keskiarvon käyttö harvinaista. Näitä lukuja käytetään lähinnä kasvuilmiöihin ja indeksilaskentaan liittyvissä erikoistapauksissa.

Geometrinen keskiarvo (\( G \)G) voidaan laskea seuraavasta kaavasta:

$$ G = \sqrt[n]{x_1 \cdot x_2 \cdot \ldots \cdot x_n} $$
geometrisen keskiarvon laskukaava

Tässä kaavassa \( n \) n viittaa havaintojen määrään ja \( {x_1} \) x 1 ensimmäisen havainnon arvoon, \( {x_2} \) x 2 toisen havainnon arvoon jne. Geometrisessa keskiarvossa siis kaikki havaintojen arvot kerrotaan keskenään ja saadusta tuloksesta otetaan \( n \) n :s juuri. Geometrista keskiarvoa voidaan käyttää hyväksi esimerkiksi laskettaessa hintaindeksistä keskimääräistä vuotuista hintatason nousua.

Harmoninen keskiarvo (\( H \)H) lasketaan kaavasta:

$$ H = {n\over {1\over{x_1}} + {1\over{x_2}} + \ldots + {1\over{x_n}} }$$
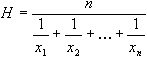
harmonisen keskiarvon laskukaava

Kaavassa \( n \) n viittaa jälleen havaintojen määrään. Samoin kuin geometrisella keskiarvolla, harmonisella keskiarvolla on sovelluksia indeksilaskennassa.