Regressioanalyysi - SPSS-harjoitus 3

Jos olet ensimmäistä kertaa aloittamassa SPSS-harjoitusta, on ennen varsinaisen harjoituksen tekemistä syytä tutustua opiskeluohjeisiin.

Tässä harjoituksessa käytetään European Values Study 2017 -tutkimuksen Suomen osa-aineistoa, osaEVS.

Havaintoaineiston hakemisesta SPSS-ohjelmaan on erilliset ohjeet.

Logistinen regressio

Regressiomalleissa, joissa selitettävä muuttuja on dikotominen (kaksiluokkainen, arvoja 0 ja 1 saava), tulkitaan selitettävän muuttujan odotusarvon riippuvan selittävistä muuttujista (Xk). Erona tavanomaiseen regressioanalyysin on se, että muuttujien välisten riippuvuuksien ei tarvitse olla nimenomaan lineaarisia, vaan myös muunlaiset riippuvuussuhteet (esimerkiksi eksponentiaalinen tai logaritminen) kelpaavat. Todennäköisyyttä sille, että havainto saa arvon 0 (tai 1) selitettävässä muuttujassa, arvioidaan logistisella mallilla:

exp(u)/(1+exp(u)), missä u = a + b₁x₁ + b₂x₂ +...+ b_kx_k

$$ {exp(u) \over (1+exp(u))} \, , missä \quad u = a + b_1 x_1 + b_2 x_2 + \ldots + b_k x_k $$

Kaavassa k on selittävien muuttujien lukumäärä, a on vakiotermi ja b_i$ b_i $:t regressiokertoimia.

Logistisen regressioanalyysin esimerkissä tutkitaan, mitkä tekijät vaikuttavat talouskasvun asettamiseen ympäristönsuojelun edelle. Aineistossa on kysymys, jossa vastaajien piti valita kahdesta vaihtoehdosta mielestään parempi (q57).

Nämä vaihtoehdot olivat:

Ympäristön suojeleminen tulisi asettaa etusijalle, vaikka se hidastaakin talouskasvua ja vie joitakin työpaikkoja ja
Talouskasvu ja työpaikkojen luominen pitäisi asettaa etusijalle, vaikka ympäristö kärsiikin siitä jossain määrin.

Vastaajista 86 % valitsi jommankumman näistä vaihtoehdoista ja 14 % vastasi jotain muuta tai ei halunnut valita näiden väliltä. Logistista regressiota varten selitettävää muuttujaa on kuitenkin kohdeltava kaksiluokkaisena, joten arvot 8 "En osaa sanoa", 9 "Ei vastausta" ja 3 "Muu vastaus" koodataan puuttuvaksi tiedoksi. Näin voidaan tutkia, mitkä tekijät vaikuttavat vastaajien todennäköisyyteen asettaa talouskasvu ympäristönsuojelun edelle.

Analyysin selittäjinä käytetään viittä eri muuttujaa:

Demografisista muuttujista mukana ovat vastaajan ikä (ika2017, koodattu syntymävuosimuuttujasta, ks. muuttujamuunnosharjoitus 1) ja sukupuoli (q63, koodattu seuraavasti: mies=0, nainen=1).
Vastaajan tulotasoa mitataan 10-luokkaisella muuttujalla (q98, arvot 88 ja 99 koodataan puuttuvaksi tiedoksi), jossa suuret arvot tarkoittavat korkeampia tuloja.
Asennemuuttujista mukana on vastaajien suhtautuminen ympäristönsuojeluun. Tämä on summamuuttuja (ympsuo) muuttujista q56_1 – q56_5 (ensimmäisen muuttujan asteikko käännettynä), jossa matalat arvot kertovat kielteisestä ja korkeammat arvot positiivisesta suhtautumisesta ympäristönsuojeluun (arvot 8 ja 9 koodataan puuttuvaksi tiedoksi).
Lisäksi mallissa on mukana muuttuja, joka kuvaa vastaajan sijoittumista politiikan vasemmisto-oikeisto -ulottuvuudella (q31, arvot 88 ja 99 koodataan puuttuvaksi tiedoksi). Se saa arvoja yhdestä kymmeneen pienten arvojen kuvastaessa sijoittumista vasemmalle.

Logistinen regressioanalyysi aloitetaan valikosta Analyze - Regression - Binary Logistic...

Seuraavassa ikkunassa valitaan selitettävä muuttuja (Dependent) ja selitettävät muuttujat (Covariates). Method-valinnalla valitaan käytettävä selittävien muuttujien lisäystapa regressiomalliin. Valittavana on suora (Enter) muuttujien lisäys sekä useita askeltavia valintamalleja. Askeltavissa menetelmissä muuttujat lisätään tai poistetaan mallista sen mukaan mikä valinta kasvattaa mallin selitysastetta parhaiten. SPSS sisältää seuraavat menetelmät:

Forward: Lähdetään tyhjästä mallista ja lisätään se muuttuja, joka parantaa selitysastetta eniten. Lopetetaan sitten, kun selitysaste ei enää parane.
Backward: Lähdetään kaikista selittävistä muuttujista ja poistetaan se muuttuja, joka vähiten heikentää selitysastetta.

Sekä etenevälle (forward) että takautuvalle (backward) menettelylle on vielä eri tapoja laskea, sisällytetäänkö muuttuja malliin vai ei (esim. Forward LR, joka lisää muuttujan malliin, jos se parantaa mallin log likelihood -lukua). Eri menetelmät eivät välttämättä päädy samaan selittävien muuttujien joukkoon. Automaattisten askeltavien menetelmien käyttöä on kritisoitu, sillä niissä ei pohdita muuttujia sisällöllisesti teorian kautta, vaan katsotaan vain niiden selitysvoimaa, jolloin teorian kannalta olennaisia muuttujia saattaa jäädä mallista pois.

Selittäviä muuttujia voi lisätä myös itse erillisinä ryhminä tai blokkeina käyttämällä Next-näppäintä. Näin voi tarkastella, kuinka paljon kukin muuttujaryhmä lisää mallin selitysvoimaa. Lisätään tässä harjoituksessa kuitenkin kaikki muuttujat malliin kerralla.

Logistinen regressioanalyysi - muuttujien valinta

Categorical-painikkeella voi määrittää selittäviä muuttujia kategorisiksi ja asettaa niille referenssikategorian, eli luokan, johon muita luokkia verrataan. Tämä on tärkeää, kun käytetään ei-numeerisia selittäviä muuttujia, koska SPSS:n logistinen regressio kohtelee selittäviä muuttujia oletuksena numeerisina. Ei-numeeristen muuttujien käyttö numeerisina voi olla tulosten tulkinnan kannalta ongelmallista ja liittyy osaltaan laajempaan keskusteluun, siitä, kuinka ei-numeerisia muuttujia tulisi analysoida ja tulkita.

Tässä harjoituksessa ei erikseen käydä läpi useampiluokkaisten kategoristen muuttujien tulkintaa (ks. dummy-muuttujien tulkinnasta lisää luvusta Lineaarinen regressioanalyysi). Selittäviä muuttujiamme kohdellaan esimerkin yksinkertaistamiseksi numeerisina sukupuolimuuttujaa lukuun ottamatta. Sukupuolimuuttuja on dikotominen dummy-muuttuja (eli se saa vain kaksi arvoa, 0 tai 1), joten sitä ei ole pakko erikseen määrittää kategoriseksi.

Options-valikosta voidaan tehdä esimerkiksi lisävalintoja mallin sopivuuden arviointiin (Classification plots, Hosmer-Lemeshow -testi). Valitaan tässä esimerkissä kuitenkin vain CI for exp(B). Tällä valinnalla lisätään tulostaulukkoon kerrointen (riskien) luottamusvälit. Oletuksena on 95 %:n luottamusväli, mutta merkitsevyystasoa voi halutessaan muuttaa.

Tulosten tulkinta

Klikkaamalla Options-valikossa Continue ja sitten OK saamme logistisen regressioanalyysin tulokset. Ensimmäiseksi ohjelma tulostaa 'Block 0: Beginning Block' otsikon alle tulokset mallista ilman selittäviä muuttujia. Tätä voi käyttää vertailutarkoituksiin, mutta kiinnostuksen kohteena ovat ensisijaisesti osion 'Block 1: Method = Enter' tulokset, jotka esitetään oheisissa kuvissa.

Logistinen regressioanalyysi - selityaste

Omnibus Tests of Model Coefficients -taulukon alin rivi kertoo, että malli on tilastollisesti merkitsevästi (p < 0,001) parempi kuin pelkän vakiotermin sisältävä malli. Model Summary -taulukossa esitetään -2 Log likelihood -arvo ja kaksi pseudoselitysarvoa, Coxin ja Snellin R² ja Nagelkerken R². Näillä pyritään esittämään, kuinka paljon riippumattomat muuttujat selittävät riippuvan muuttujan varianssista. Näillä ei kuitenkaan ole suoraa prosentuaalista tulkintaa, kuten lineaarisessa regressiomallissa. Nagelkerken R² saa arvoja välillä 0-1 ja voidaan sanoa, että arvot lähempänä yhtä kertovat paremmasta selitysarvosta. Tässä tapauksessa mallin selitysaste (0,32) ei ole erityisen korkea.

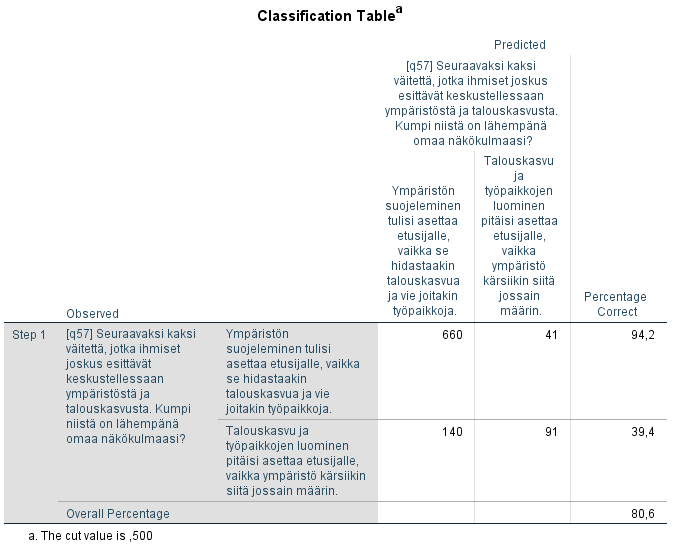
Taulukosta Classification Table voidaan arvioida mallin hyvyyttä eli oikein luokiteltujen havaintojen määrä. Mallin antaman ennusteen P avulla voidaan kukin havainto luokitella kahteen ryhmään: Jos p < 0.5, niin ennustetaan, että havainto kuuluu ryhmään 0 ja vastaavasti, jos p > 0.5, niin ennustetaan, että havainto kuuluu ryhmään 1. Ympäristön suojelua kannattavien ryhmässä oikein luokiteltiin 94 prosenttia ja talouskasvua kannattavien ryhmässä vain 39 prosenttia. Kokonaisuudessaan oikein luokiteltiin 81 prosenttia havainnoista, mikä on melko hyvä taso. Ilman selittäviä muuttujia oikein luokiteltiin 75 % havainnoista, joten malli parantaa havaintojen ennustettavuutta hieman.

Logistinen regressioanalyysi - mallin hyvyys

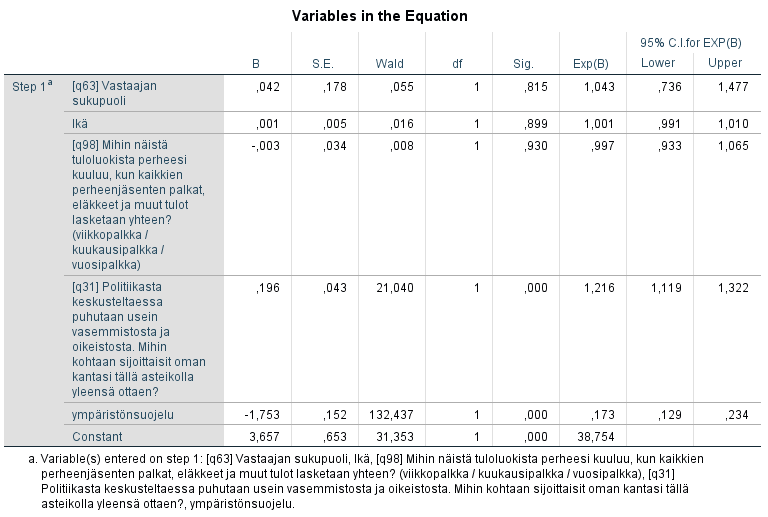
Taulun Variables in the Equation sarakkeessa B luetellaan regressiokertoimet. Regressiokertoimia vastaavat testit perustuvat Waldin testisuureeseen, joka saadaan jakamalla kerroin (B) keskivirheellään (S.E.) ja korottamalla ko. osamäärä toiseen potenssiin. Siis esim. Waldin testisuure sukupuolimuuttujan (q63) kertoimelle on:

(0,041649/ 0,177643)² ≈ 0,055

$$ {\left( 0.041649 \over 0.177643 \right) ^2} \approx 0.055 $$

Logistinen regressioanalyysi - tulokset

Waldin testisuure on $ x_2 $ -jakautunut vapausastein 1. (Mikäli selittävä muuttuja on luokkamuuttuja, on vapausaste m - 1, missä m on luokkien määrä.) Sig. -sarakkeesta näemme Waldin-testisuureen arvoa vastaavan p-arvon. Toteamme, että riippuvista muuttujista sijoittuminen vasemmisto-oikeisto -asteikolla ja suhtautuminen ympäristönsuojeluun ovat tilastollisesti merkitsevästi (alfa = 0,05) nollasta poikkeavia.

Waldin testi on suurilla regressiokertoimien arvoilla epäluotettava. Tällöin nimittäin estimoitu keskivirhe on liian suuri, joten Wald-testisuure itse on liian pieni, ja tämä saattaa johtaa siihen, että nollahypoteesi: B_i = 0 jää voimaan silloinkin, kun se pitäisi hylätä. Suositeltava vaihtoehto Waldin testille suurilla kertoimien arvoilla on testata, muuttuuko logaritminen uskottavuus (log likelihood), kun kyseinen muuttuja lisätään malliin.

Kertoimet (B) eli riskit on helpointa tulkita vetosuhde -käsitteen (odds ratio) avulla, jota ylläolevassa tulostuksessa vastaa sarake Exp(B). Tämä osoittaa kutakin muuttujaa vastaavan riskin muutoksen: Jos yksittäisen havainnon jonkin muuttujan arvo lisääntyy yhdellä yksiköllä, niin kyseisen havainnon uusi riski saadaan kertomalla alkuperäinen riski vastaavalla odds ratio -kertoimella.

Jos esimerkiksi vasemmisto-oikeisto -asteikolla liikutaan yksi askel oikealle (kohti suurempia arvoja), uusi veto (odds) saadaan vanhasta kertomalla se luvulla 1,216. Toisin sanoen, riski kasvaa 21,6 prosenttia. Tätä voidaan tulkita niin, että jokainen yhden yksikön kasvu asteikolla lisää todennäköisyyttä valita talouskasvua suosiva vaihtoehto 21,6 prosentilla.

Tuloksia tarkastellessa on tärkeää muistaa muuttujien asteikko, eli mitä pienet ja suuret arvot tarkoittivat, jotta tulkinnat tehdään "oikeaan suuntaan". Sama koskee kategorisia ja dikotomisia selittäviä muuttujia. Sukupuoli ei ollut esimerkissä tilastollisesti merkitsevä, mutta jos se olisi ollut, olisimme verranneet naisia miehiin, koska referenssikategoriana oli naiset. Jos tulkinta tuntuu hankalalta, muuttujia voi nimetä uudelleen helpottamaan tulkintaa (esim. tässä esimerkissä sukupuolimuuttujan nimeksi 'naiset').

Kahdessa viimeisessä sarakkeessa esitetään kertoimien (B) luottamusvälien ala- ja ylärajat. Esimerkiksi vasemmisto-oikeisto -asteikon kohdalla luottamusväli on 1,119–1,322, mikä tarkoittaa, että valitsemallamme riskitasolla on 5 %:n mahdollisuus, että kertoimen arvo on välin ulkopuolella.