Regressioanalyysi - SPSS-harjoitus 4

Jos olet ensimmäistä kertaa aloittamassa SPSS-harjoitusta, on ennen varsinaisen harjoituksen tekemistä syytä tutustua opiskeluohjeisiin.

Tässä harjoituksessa käytetään Joop Hoxin popular.sav -aineistoa.

Hierarkkinen lineaarinen regressioanalyysi SPSS-ohjelmistolla

Tässä harjoituksessa rakennetaan hierarkkinen lineaarinen regressiomalli, jossa selitetään oppilaan omaa arviota siitä, miten suosittu hän on koulussa. Selittävinä muuttujina ovat oppilaan sukupuoli ja opettajan työkokemuksen pituus. Harjoitus perustuu Joop Hoxin kirjan Multilevel Analysis. Techniques and Applications ensimmäisen painoksen (2002) harjoitukseen ja aineistoon. Harjoituksessa käytetty aineisto (popular.sav) on ladattavissa Hoxin kotisivuilta (Avautuu uuteen välilehteen) .

Lataa aineisto seuraavasti:

Mene osoitteeseen joophox.net/mlbook1/leabook.htm (Avautuu uuteen välilehteen)
Valitse kohdasta "The data sets used for the examples..." linkki SPSS/Windows
Tallenna linkistä avautuva spsssav.zip -tiedosto koneellesi
Pura pakattu tiedosto käyttäen jotain sopivaa purkuohjelmaa (esim. 7-Zip)
Tiedostosta purkautuu useita tiedostoja. Paikallista spsssav -alikansiosta tiedosto popular.sav
Avaa popular.sav SPSS-ohjelmaan

Hoxin kotisivuilta on ladattavissa myös kirjan toisessa painoksessa (2010) käytetty aineisto (popular2.sav). Tähän aineistoon liittyen sivuilta on ladattavissa video-ohjeet hierarkkisen lineaarisen mallin rakentamiseen SPSS-ohjelman lisäksi useilla muilla ohjelmilla (HLM, MLwiN, R ja MPlus). Aineistot, videot ja kotisivuilta löydettävä muu materiaali ovat vapaasti käytettävissä.

Aineistonkuvaus
Harjoituksen aineisto (popular.sav): 100 luokkaa, 2000 oppilasta.
Selitettävä muuttuja: oppilaan arvio siitä, miten suosittu hän on koulussa (0–10)
Selittäjä yksilötasolla: oppilaan sukupuoli (0 = poika, 1 = tyttö)
Selittäjä ryhmätasolla: koululuokka ja sen opettajan työkokemus vuosina (2–25)

Nollamalli (Intercept only model)

Hierarkkiset mallit on hyvä aloittaa aina niin sanotulla nollamallilla. Nollamallissa ei ole mukana vielä selittäviä muuttujia. Nollamallissa selvitetään, missä määrin vaste- eli selitettävän muuttujan varianssi jakautuu yksilötasolle ja ryhmätasolle, jotka tässä harjoituksessa ovat oppilas ja koululuokka. Nollamallissa on siis mukana vain vakio ja virhetermit:

Popularity_ij = γ₀₀ + u_0j + e_ij

$$ Popularity_{ij} = \gamma_{00} + u_{0j} + e_{ij} $$

Hierarkkinen lineaarinen malli rakennetaan SPSS-valikosta Analyze – Mixed Models – Linear... Mallin rakentaminen alkaa aineiston rakenteen määrittämisellä.

Ensin määritellään ryhmätason muuttuja. Tässä aineistossa se on school identification number. Muuttuja lisätään kohtaan Subjects:

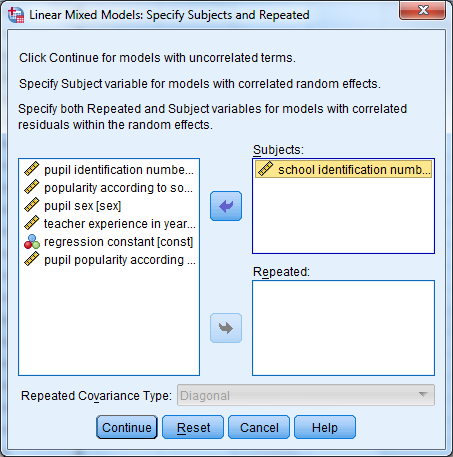
Klikkaa Continue.

Sitten määritellään vastemuuttuja, joka tässä aineistossa on popularity according to sociometric score. Muuttuja lisätään kohtaan Dependent variable.

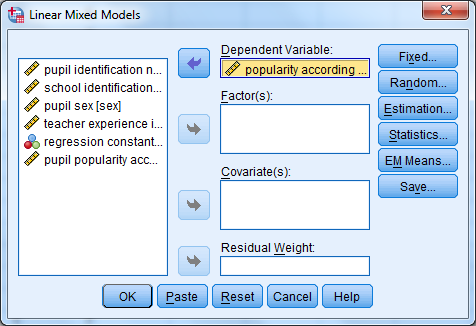
Seuraavaksi määritellään virhetermien jakautuminen kahteen erilliseen varianssikomponenttiin; yksilötason varianssiin ja ryhmätason varianssiin. Tämä tehdään välilehdellä Random. Välilehdellä kohdassa Subject groupings näkyy jo määritelty ryhmittelevä muuttuja kohdassa Subjects. Muuttuja tulee siirtää myös kohtaan Combinations. Lisäksi välilehdeltä valitaan kohta Include intercept. Malliin otetaan siis mukaan varianssikomponenttien lisäksi myös vakio.

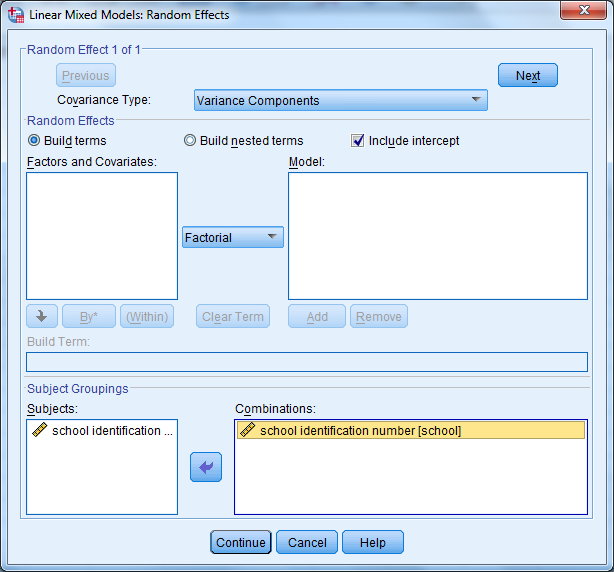
Klikkaa Continue.

Ennen nollamallin laskemista SPSS voi laskea vielä kaikille mallin parametreille estimaatit. Tämä tapahtuu välilehdellä Statistics, jossa valitaan kohta Parameters Estimates.

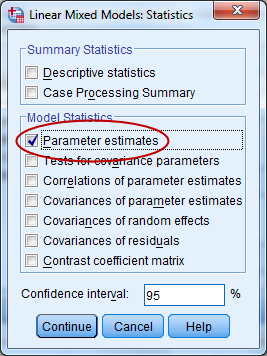
Klikkaa Continue ja OK.

Tulosikkuna

Avautuvassa tulosikkunassa nähdään ensin laatikko Model Dimension, jossa kuvataan mallissa olevien tasojen ja parametrien määrä. Seuraava laatikko Information Criteria sisältää mallin hyvyyttä kuvaavia arvoja. Seuraavasta laatikosta Type III Test of Fixed Effects nähdään kiinteiden vaikutusten tilastollinen testi ja sitä seuraavasta laatikosta Estimates of Fixed Effects parametrien estimaatit. Viimeisestä laatikosta Estimates of Covariance Parameters nähdään varianssien jakautuminen.

Nollamallissa vakion estimaatti on 5,31. Se kuvaa tässä vastemuuttujan keskiarvoa kaikkien luokkien oppilailla koko aineistossa. Muuttuja saa arvoja välillä 0–10 ja mitä korkeampi arvo on, sitä suositummaksi oppilas itsensä arvioi.

Nollamalli osoittaa, missä määrin vastemuuttujan varianssi jakautuu yksilötason ja ryhmätason välille. Se nähdään tulosikkunan viimeisestä laatikosta. Yksilötason varianssia kuvataan sanalla Residual. Yksilötason varianssi on siten 0,64. Ryhmätason (tässä siis koululuokka) varianssi löytyy yksilötason varianssin alapuolelta ja se on 0,88. Jo tästä nähdään, että koululuokalla on yhdenmukaistava vaikutus oppilaiden arvioon siitä, miten suosittuja he ovat. Se, missä määrin vastemuuttujan varianssi on selitettävissä luokkaan liittyvällä ryhmätason tekijöillä, saadaan selville laskemalla sisäkorrelaatio.

Sisäkorrelaatio lasketaan jakamalla luokkatason varianssi yksilötason ja ryhmätason varianssien summalla. Eli: 0,88/(0,64+0,88) = 0,58.

Sisäkorrelaation mukaan 58 prosenttia vastemuuttujan varianssista on selitettävissä luokkatason selittäjillä. Tällöin 42 prosenttia vastemuuttujan varianssista on selitettävissä yksilötason selittäjillä. Koululuokan vaikutus on siis varsin merkittävä.

Yksilötason selittäjien lisääminen malliin

Seuraavassa vaiheessa lisätään malliin yksilötason selittäjä eli sukupuoli. Tämä tehdään ensin pitämällä sukupuolen vaikutus kiinteänä. Kiinteillä vaikutuksilla tarkoitetaan siis sitä, että kullakin analyysissä olevalla ryhmällä – tässä koululuokalla – on oma regressiosuoransa ja oma vakionsa, mutta regressiokertoimen kulmakerroin on kiinteä. Tätä kutsutaan random intercept -malliksi:

Popularity_ij = γ₀₀ + γ₁₀sex_ij + u_0j+ e_ij

$$ Popularity_{ij} = \gamma_{00} + \gamma_{10} sex_{ij} + u_{0j} + e_{ij} $$

Nollamallissa määriteltiin valmiiksi aineiston rakenne ryhmittelevän muuttujan, varianssien jakamisen yms. osalta, joten näitä ei tarvitse määritellä uudelleen. Jatketaan nyt mallin rakentamista: Analyze – Mixed Models – Linear + Continue.

Lisätään sukupuolimuuttuja (pupil sex) kohtaan Covariate(s). Ne selittäjät, jotka ovat jatkuvia muuttujia, lisätään lähtökohtaisesti kohtaan Covariate(s) ja taas kategoriset (eli luokittelu- tai järjestysasteikolliset) muuttujat kohtaan Factor(s). Kaksiluokkaisen muuttujan kohdalla ei kuitenkaan ole merkitystä, kumpaan kohtaan muuttujan lisää. Käsitellään sukupuolta tässä siinä mielessä jatkuvana muuttujana, että lisätään se kohtaan Covariate(s).

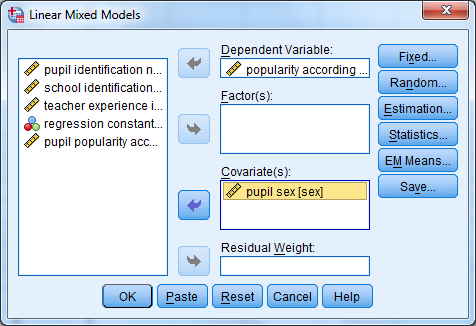
Sukupuoli on nyt otettu mukaan malliin, mutta se tulee vielä erikseen lisätä selittäjäksi. Tämä tehdään välilehdellä Fixed. Siirrä sex-muuttuja myös kohtaan Model Add -painikkeella. Välilehden keskellä olevasta valikosta valitaan "vaikutustyyppi". Vaihtoehtoina ovat suora vaikutus (Main Effects) sekä interaktiovaikutus (Interaction). Mikäli selittäjä on kategorinen, myös se tulee merkitä tästä valikosta (Factorial). Tässä mallissa sukupuolen vaikutusta tarkastellaan suorana vaikutuksena.

Klikkaa Continue ja OK.

Tulosikkuna

Mallin kiinteiden parametrien estimaatit näkyvät jälleen laatikossa Estimates of Fixed Effects. Sukupuolen estimaatti on 0,84. Muuttuja oli koodattu niin, että 0 = poika ja 1 = tyttö, joten tytöt arvioivat olevansa keskimäärin poikia suositumpia. Estimaattia tulkitaan siis samoin, kuin tavallisessa lineaarisessa regressioanalyysissä. Sukupuolen vaikutus on tilastollisesti merkitsevä: se nähdään sekä p-arvosta että luottamusvälistä.

Sukupuolella on siis merkitsevä yhteys vastemuuttujaan, mutta missä määrin se selittää vastemuuttujan varianssia toisaalta yksilötasolla ja toisaalta ryhmätasolla? Nollamallissa yksilötason varianssi oli 0,64 ja luokkatason varianssi 0,88. Nyt yksilötason varianssi on 0,46 ja luokkatason varianssi 0,86. Jo variansseista nähdään, että erityisesti yksilötason varianssi laski: sukupuolen mukaan tuominen selittää siis vastemuuttujan varianssia yksilötasolla. Varianssien perusteella voidaan laskea tarkka selitysosuus sille, missä määrin sukupuolen mukaan tuominen selittää eri tason variansseja.

Muutos varianssista saadaan laskettua kaavalla:

R² = σ²_lähtötaso - σ²_vertailu / σ²_lähtötaso

$$ R^2 = {\sigma^2_{lähtötaso} - \sigma^2_{vertailu}\over\sigma^2_{lähtötaso}} $$

Yksilötasolla (oppilas):

R²₁ = 0,64 - 0,46 / 0,64 = 28 %

$$ R^2_1 = { 0.64 - 0.46 \over 0.64 } = 28\% $$

Luokkatasolla (koululuokka):

R²₂ = 0,88 - 0,86 / 0,88 = 3 %

$$ R^2_2 = {0.88 - 0.86 \over 0.88} = 3\% $$

Sisäkorrelaation avulla saimme nollamallin jälkeen selville, että vastemuuttujan kokonaisvarianssista 58 prosenttia selittyy luokkatason tekijöillä ja 42 prosenttia yksilötason tekijöillä. Yksilötason varianssista 28 prosenttia selittyy sukupuolella. Ryhmätason varianssista kolme prosenttia selittyy sukupuolella. Sukupuolen mukaan tuominen selittää siis suhteellisen paljon yksilöiden välistä eroa, mutta ei koululuokkien välistä eroa.

Ryhmätason selittäjien lisääminen malliin

Seuraavaksi malliin lisätään ryhmätason muuttuja. Tässä analyysissä se on opettajan työkokemus vuosina (teacher experience in years).

Popularity_ij = γ₀₀ + γ₁₀sex_ij + γ₀₁t.exp._j + u_0j + e_ij

$$ Popularity_{ij} = \gamma_{00} + \gamma_{10} sex_{ij} + \gamma_{01} t.exp._j + u_{0j} + e_{ij} $$

Jatketaan mallin rakentamista: Analyze – Mixed Models – Linear + Continue. Lisätään uusi selittäjä eli teacher experience in years mukaan kovariaattina, koska kyseessä on jatkuva muuttuja.

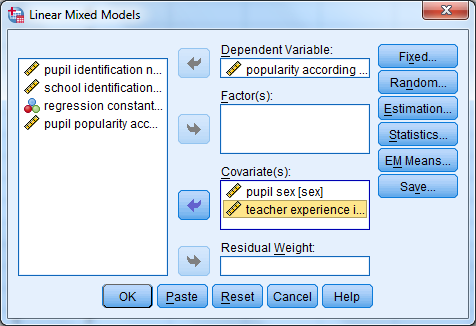
Jotta uusi muuttuja tulee selittäjänä mukaan malliin, se pitää lisätä päävaikutuksena (Main Effects) malliin välilehdellä Fixed. Siirrä texp-muuttuja myös kohtaan Model Add -painikkeella.

Klikkaa Continue ja OK.

Tulosikkuna

Tulosikkunan mukaan opettajan työkokemuksen pituutta kuvaavan muuttujan estimaatti on 0,09. Estimaatti ei ole erityisen suuri, mutta tilastollisesti merkitsevä. Oppilaat siis arvioivat olevansa sitä suositumpia, mitä kokeneempi opettaja heillä on.

Opettajan kokemuksen mukaan tuominen malliin ei vaikuta ollenkaan yksilötason varianssiin. Sen sijaan luokkatason varianssi laskee selvästi arvosta 0,88 arvoon 0,49. Arvojen perusteella voidaan jälleen laskea, paljonko opettajan kokemus selittää luokkien välistä eroa vastemuuttujassa. Vertailun lähtökohdaksi otetaan jälleen nollamallin varianssi.

R²₂ = 0,88 - 0,46 / 0,88 = 48%

$$ R^2_2 = {0.88 - 0.46 \over 0.88} = 48\% $$

Vastemuuttujan varianssista 58 prosenttia oli alun perin selitettävissä luokkatason tekijöillä. 48 prosenttia tästä osuudesta selittyy opettajan kokemuksella.

Satunnaiskertoimien malli

Kiinteiden vaikutusten selvittämisen jälkeen on usein syytä tarkastella sitä, pidetäänkö yksilötason selittäjien vaikutukset lopullisessa mallissa kiinteinä, vai tuleeko joku selittäjistä huomioida satunnaisvaikutuksena. Tässä mallissa sukupuoli on ainoa yksilötason muuttuja ja sen vaikutusta on tähän mennessä tarkasteltu kiinteänä. Nyt tarkastellaan sukupuolen vaikutusta satunnaisvaikutuksena. Eli otetaan huomioon myös se, että sukupuolen ja vastemuuttujan välinen yhteys voi olla erilainen eri luokissa. Annetaan siis regressiokertoimien vaihdella satunnaisesti ja tarkastellaan, onko tämä muutos malliin tilastollisesti merkitsevä.

Mikäli mallissa on useampia yksilötason tason selittäjiä, tämä tarkastelu on syytä tehdä kaikille erikseen. Mikäli selittäjän "vapauttaminen" satunnaisvaikutukseksi ei tuo merkityksellistä muutosta malliin, on sen vaikutus hyvä pitää kiinteänä.

Satunnaiskertoimien malli (random coefficient model):

Popularity_ij = γ₀₀ + γ₁₀sex_ij + γ₀₁t.exp._j + u_0j + u_1jsex_ij + e_ij

$$ Popularity_{ij} = \gamma_{00} + \gamma_{10} sex_{ij} + \gamma_{01} t.exp._j + u_{0j} + u_{1j}sex_{ij} + e_{ij} $$

Jatketaan jälleen mallin rakentamista: Analyze – Mixed Models – Linear + Continue. Satunnaistermin lisääminen tapahtuu välilehdellä Random. Lisätään sukupuoli (sex) malliin satunnaisterminä. Siirrä sex -muuttuja myös kohtaan Model Add -painikkeella. Muista vaihtaa oletuksena oleva Factorial päävaikutukseksi Main Effects.

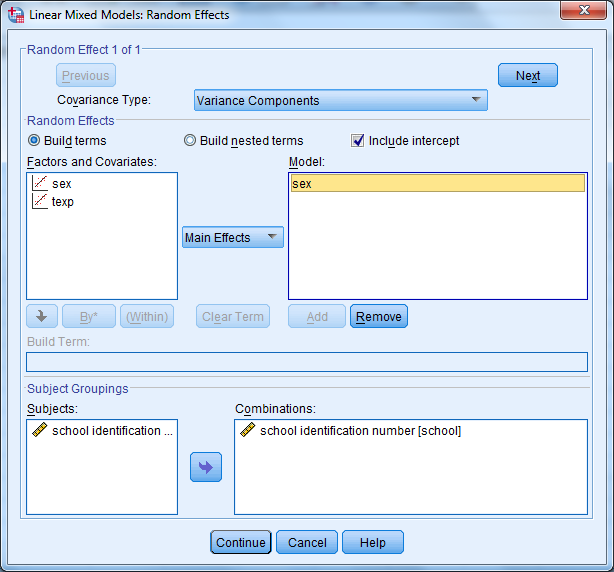
Satunnaistermien lisäämisen yhteydessä tulee estimoida myös vakion ja regressiokertoimen välinen kovarianssi. Tämä tapahtuu niin ikään Random -välilehdellä. Valitse kovarianssityypiksi Unstructured ja paina Continue. SPSS voi laskea myös kovarianssin tilastollisen merkitsevyyden suoraan. Tämä määritellään välilehdellä Statistics.

Klikkaa Continue ja OK.

Tulosikkuna

Satunnaistermejä kuvaavaan laatikkoon on nyt tullut uusia termejä. Kuten aiemminkin, Residual viittaa yksilötason varianssiin (0,39) ja sen jälkeinen arvo (0,41) ryhmätason varianssiin. Nyt sitä merkitään UN (1,1) merkinnällä. UN (2,1) on kovarianssitermi ja UN (2,2) viittaa luokkien välisten regressiokertoimien vaihteluun (slope variation). Sitä merkitään usein termillä ϭ²_u1. Termin tilastollisesta testistä nähdään, onko regressiokertoimien välinen vaihtelu ryhmien välillä tilastollisesti merkitsevää.

Regressiokertoimien vaihtelu luokkien välillä ja sen merkitsevyys on asia, jota halutaan arvioida yksilötason selittäjien muuttamisella satunnaisvaikutukseksi: vaihteleeko selittäjän ja vastemuuttujan välinen yhteys tilastollisesti merkitsevästi luokkien välillä. Luokkien välinen vaihtelu tässä analyysissä on 0,27 ja se on tilastollisesti merkitsevää. Se tarkoittaa sitä, että sukupuolimuuttujan estimaattia 0,84 ei tule tulkita huomioimatta tätä. Jos käytämme estimaattia 0,84, väitämme estimaatin olevan sama (kiinteä) kaikille luokille. Analyysimme osoittaa, että näin ei kuitenkaan ole. Satunnaistermin merkityksellisyydestä kertoo myös se, että ryhmätason varianssi laski arvoon 0,41.

Luokkien välisen yhteyden vaihtelua voi kuvata vielä tarkemmin tämän mallin perusteella, mutta se on monimutkaista. Vaihtelun suuruutta voidaan laskea hyödyntämällä parametrin hajontaa, mutta tässä ei perehdytä siihen. Asiasta voi lukea lisää Hoxin teoksesta (2010, 19). Nyt mukana mallissa on myös kovarianssitermi. Kovarianssi jätetään hyvin usein tulkitsematta, emmekä siksi perehdy siihen tässä. Se on kuitenkin syytä pitää mallissa mukana (Hox 2010, 18).

Satunnaiskertoimien malli interaktiolla

Lopuksi satunnaiskertoimien malliin lisätään vielä "cross-level" interaktio-termi. Tarkastellaan, vaikuttaako opettajan työkokemus vuosina siihen, miten sukupuoli vaikuttaa oppilaan arvioon siitä, miten suosittu hän on. Tämä on helppo tapa avata hieman edellisen vaiheen tulosta siitä, että sukupuolen ja vastemuuttujan välinen yhteys vaihtelee luokkien välillä.

Popularity_ij = γ₀₀ + γ₁₀sex_ij + γ₀₁t.exp._j + γ₁₁sex_ijt.exp._j + u_0j + u_1jsex_ij + e_ij

$$ Popularity_{ij} = \gamma_{00} + \gamma_{10} sex_{ij} + \gamma_{01} t.exp._j + \gamma_{11} sex_{ij} t.exp._j + u_{0j} + u_{1j}sex_{ij} + e_{ij} $$

Jatketaan mallia: Analyze – Mixed Models – Linear + Continue. Interaktion termin lisääminen tapahtuu välilehdellä Fixed. Valitse vaikutukseksi interaktio ja lisää muuttujat sex ja texp samaan aikaan malliin (pidä CTRL-näppäin pohjassa valitessasi muuttujia).

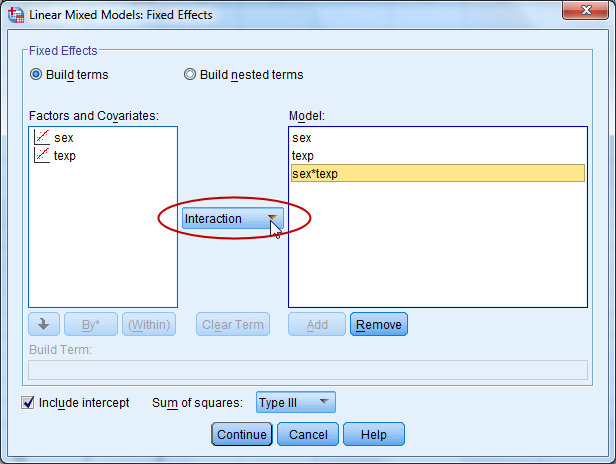
Klikkaa Continue ja OK.

Tulosikkuna

Interaktio-termin myötä sukupuolen vaikutusta kuvaava estimaatti nousi arvoon 1,3. Tytöt kokevat siis itsensä suositummiksi kuin pojat. Interaktio-termi saa oman estimaattinsa, joka on -0,03. Se on varsin pieni, mutta tilastollisesti merkitsevä. Negatiivinen arvo viittaa siihen, että luokissa, joissa on kokenut opettaja, tytöt eivät koe olevansa niin paljon suositumpia kuin pojat. Erot tyttöjen ja poikien itsearvioissa siis pienenevät opettajan kokemuksen kasvaessa.

Kun katsotaan luokkien välisten regressiokertoimien vaihtelua kuvaavaa arvoa, se laski edellisen mallin arvosta 0,27 arvoon 0,23. Interaktion lisääminen malliin siis selitti luokkien välisiä eroja regressiokertoimissa. Myös tälle voidaan laskea selitysosuus:

R²₃ = 0,27 - 0,23 / 0,27 = 15 %

$$ R^2_3 = { 0.27 - 0.23 \over 0.27 } = 15\% $$

Tulosten raportointi

Analyysin tulokset on raportoitu taulukossa 1. Tulosten esittämistavalle ei ole olemassa yhtä selkeää mallia, mutta on hyvä raportoida kaikki eri mallit erikseen. Siten lukijan on helppo seurata muutoksia estimaateissa ja variansseissa. Taulukossa on lisäksi raportoitu mallin hyvyyttä kuvaava -2LL -arvo kaikkien eri vaiheiden osalta. Vaihtoehtoisesti tässä olisi voitu raportoida esimerkiksi AIC- tai BIC-informaatiokriteerin arvo.

Taulukko 1. Oppilaan sukupuolen ja opettajan työkokemuksen pituuden vaikutus oppilaan arvioon siitä, miten suosittu hän on koulussa.
	Nollamalli	Kiinteiden vaikutusten malli (yksilötason muuttuja)	Kiinteiden vaikutusten malli (luokkatason muuttuja)	Satunnais-kertoimien malli	Satunnais-kertoimien malli + interaktio
Kiinteä osa
Vakio	5.31	4.90 (.10)	3.56 (.17)	3.34 (.16)	3.31 (.16)
Sukupuoli		0.84 (.03)	0.84 (.03)	0.84 (.06)	1.33 (.13)
Opettajan kokemus			0.09 (.01)	0.11 (.01)	0.11 (.01)
Sp*OpeKokemus					-0.03 (.01)
Satunnainen osa
σ²_e	0.64 (.02)	0.46 (.01)	0.46 (.01)	0.39 (.01)	0.39 (.01)
σ²_u0	0.88 (.13)	0.86 (.13)	0.49 (.07)	0.41 (.06)	0.41 (.06)
σ²_u1				0.27 (.05)	0.23 (.04)
σ_u01				0.02 (.04)	0.02 (.04)
-2LL	5116	4493	4444	4276	4268

Taulukon 1 perusteella voidaan todeta, että tytöt kokevat itsensä keskimäärin suositummiksi kuin pojat. Myös opettajan työkokemuksen pituudella on vaikutusta siihen, miten suosituiksi oppilaat kokevat itsensä. Mitä kokeneempi opettaja on, sitä suositummiksi oppilaat itsensä arvioivat. Opettajan kokemus myös tasapäistää eroja tyttöjen ja poikien arvioissa. Mitä kokeneempi opettaja on, sitä vähemmän tyttöjen itsearviot heidän suosiostaan eroavat keskiarvoiltaan vastaavista poikien arvioista.