Kovarianssi ja korrelaatio
Elina Kestilä-Kekkonen (viittausohje)
Kovarianssi eli yhteisvaihtelu

Yhden muuttujan varianssilla tarkoitetaan keskimääräistä virhettä havaintojen ja keskiarvon välillä. Kun puhutaan kovarianssista, tarkastellaan kahden jatkuvan muuttujan vaihtelua samanaikaisesti eli niiden yhteisvaihtelua. Toisin sanoen kovarianssissa on kyse kahden muuttujan välisestä yhteydestä ja suhteesta.
Jos muuttujien välillä on yhteys, silloin yhden muuttujan poiketessa keskiarvosta johonkin suuntaan toisen muuttajan pitäisi poiketa keskiarvosta samaan tai täysin päinvastaiseen suuntaan. Yhteisvaihtelua tarkastelemalla voidaan tutkia muun muassa (Nummenmaa 2004):
- kahden ilmiön esiintymistä samanaikaisesti
- kahden ilmiön liittymistä toisiinsa tai
- kahden ilmiön välisiä syy-seuraussuhteita
Kovarianssikertoimella arvioidaan kahden muuttujan yhteisen vaihtelun voimakkuutta ja suuntaa. Kovarianssin laskemisen edellytyksenä on, että muuttujat ovat vähintään välimatka-asteikollisia ja normaalisti jakaantuneita. Mitä suurempi kovarianssikertoimen itseisarvo on, sitä vahvempi on muuttujien välinen yhteys (Nummenmaa 2004).
Kovarianssikerroin voi saada sekä positiivisia tai negatiivisia arvoja, ja myös arvon 0. Positiivinen kovarianssi tarkoittaa, että toisen muuttujan arvojen kasvaessa toisenkin arvot kasvavat, negatiivinen, että toisen muuttujan arvojen kasvaessa toisen muuttujan arvot pienenevät. Kovarianssin arvo nolla kertoo, ettei muuttujien välillä ole yhteyttä. Kovarianssikerroin lasketaan seuraavalla kaavalla:
Yhtälössä xi on muuttujan x i:nnen havainnon arvo ja x \( \overline x \) on muuttujan x keskiarvo. Vastaavasti yi on muuttujan y i:nnen havainnon arvo ja y \( \overline y \) on muuttujan y keskiarvo.
Kovarianssin suuruus riippuu kuitenkin muuttujan asteikosta, ja siksi kovarianssien vertailu keskenään on usein mahdotonta. Toisin sanoen kovarianssin suuruus vaihtelee esimerkiksi sen mukaan, onko muuttujan arvot mitattu kilometreinä, metreinä tai sentteinä tai sen mukaan, millaisia arvoja muuttuja voi luontaisesti saada (vrt. esim. ikä, koulutuksen pituus, asenteet).
Kovarianssilla ei myöskään ole alinta tai ylintä arvoa, jonka se voi saada. Kovarianssikertoimen perusteella ei siten voi sanoa mitään yhteyden voimakkuudesta, ainoastaan kertoimen etumerkin perusteella sen suunnasta. Niinpä kovarianssia useammin muuttujien yhteisvaihtelun tunnuslukuna käytetään standardoitua korrelaatiokerrointa, jonka perusteella voidaan tehdä päätelmiä myös yhteyden voimakkuudesta.
Kovarianssin standardointi eli korrelaatiokerroin

Korrelaatiolla tarkoitetaan kahden jatkuvan muuttujan lineaarista yhteyttä. Kovarianssin tavoin korrelaatio voi olla joko positiivinen (esim. Mitä vanhempi vastaaja on, sitä enemmän hän käyttää aikaa television katseluun), negatiivinen (Mitä enemmän vastaaja liikkuu, sitä alhaisempi on hänen verenpaineensa) tai korrelaatiota ei ole lainkaan (= 0) (Vastaajan poliittisella orientaatiolla ei ole yhteyttä siihen kuinka paljon hän syö vihanneksia).
Korrelaatiota tarvitaan siksi, että kovarianssi on riippuvainen muuttujien mitta-asteikoista. Korrelaation avulla myös asteikoltaan erilaisten muuttujien suhdetta voidaan tutkia korrelaatiolla. Korrelaatiokerroin saadaan standardoimalla muuttujien kovarianssi keskihajontaa apuna käyttäen. Jos mikä tahansa etäisyys keskiarvosta jaetaan keskihajonnalla, saadaan etäisyys keskihajontoina. Toisin sanoen, mikäli kovarianssi halutaan ilmaista standardoituna mittayksikkönä, se jaetaan molempien muuttujien keskihajonnoilla. Keskihajonnat kerrotaan tällöin keskenään. (Field 2013). Tuloksena syntyy Pearsonin tulomomenttikorrelaatiokerroin, eli Pearsonin korrelaatiokerroin (r).
lyhyemmin kaavana ilmaistuna
Pearsonin korrelaatiokerroin

Pearsonin korrelaatiokerroin on yksi yleisimpiä tunnuslukuja kun tarkastellaan kahden jatkuvan muuttujan yhteisvaihtelua. Se mittaa lineaarisen yhteyden voimakkuutta kahden muuttujan välillä. Lineaarinen yhteys tarkoittaa, että toisen muuttujan kasvaessa toinen muuttuja joko kasvaa tai pienenee. Jos muuttujien välinen suhde on esimerkiksi logaritminen tai eksponentiaalinen, suhde voidaan myös muuttaa lineaariseksi erillisin laskutoimituksin (ks. esim. Kandethody & Tsokos, 2009).
Standardoinnin tuloksena korrelaatiokerroin voi saada ainoastaan arvoja välillä -1 ja 1.
- Korrelaatiokertoimen arvo 1 kertoo täydellisestä positiivisesta yhteydestä: kun toisen muuttujan arvot kasvavat, kasvavat toisen muuttujan arvot samassa suhteessa.
- Korrelaatiokertoimen arvo -1 kertoo täydellisestä negatiivisesta yhteydestä: kun toisen muuttujan arvot kasvavat, vähenevät toisen muuttujan arvot samassa suhteessa.
- Korrelaatiokertoimen arvo 0 kertoo ettei yhteyttä ole: kun toisen muuttujan arvot muuttuvat, toisen arvot pysyvät ennallaan
Samoin kuin kovarianssia laskettaessa, on korrelaatiotakin laskettaessa syytä muistaa, että Pearsonin korrelaatiokerroin on parametrinen. Toisin sanoen muuttujien tulee olla vähintään välimatka-asteikollisia ja normaalisti jakautuneita. Havaintoja tulisi analyysissa olla vähintään 50 ja mielellään yli 100 (Nummenmaa 2004).
Mikäli otoksessa havaittu korrelaatiokerroin halutaan yleistää koskemaan koko populaatiota, voidaan tarkastella korrelaatiokertoimen tilastollista merkitsevyyttä. Kuten yleensä yhteiskuntatieteissä, päättelyä tehdään pääsääntöisesti viiden prosentin riskitasolla eli p-arvon on oltava alle 0.05, jotta tulos voitaisiin yleistää otoksesta populaatioon. Käytännössä tämä tarkoittaa sitä, että on alle viiden prosentin riski sille, ettei otoksessa havaittua korrelaatiota olekaan tutkittavassa populaatiossa.
Tilastollista merkitsevyyttä voi tarkastella myös yksinkertaisella nyrkkisäännöllä (ks. Krehbiel 2004). Korrelaation itseisarvon tulisi olla suurempi kuin 2 jaettuna otoksen tapausten lukumäärän neliöjuurella. Esimerkiksi mikäli otoksessa on 1000 vastaajaa, korrelaation itseisarvon tulisi olla suurempi kuin 2/√1000 eli suurempi kuin 0.0631.
Tilastollinen merkitsevyys on kuitenkin aina eri asia kuin käytännön merkitsevyys. Siksi kahden muuttujan yhteyden kartoittamiseksi on järkevää ennen kertoimien laskemista piirtää sirontakuvio.
Sirontakuvion tarkastelu

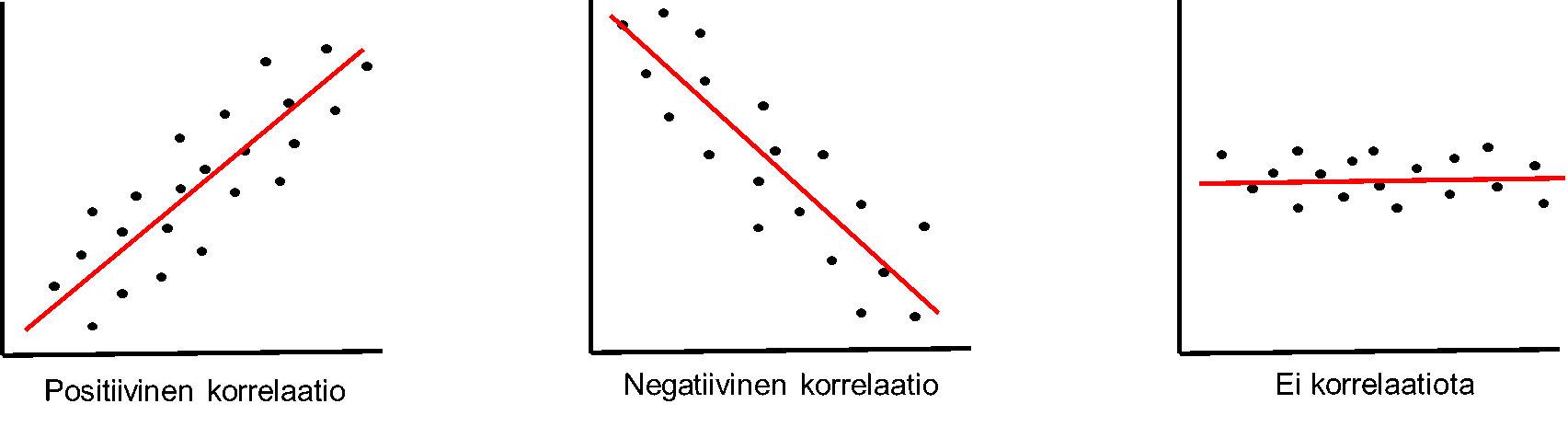
Kovarianssin ja korrelaatio tarkastelu on hyvä aloittaa aina piirtämällä sirontakuvio ja tutkimalla yhteyttä ensin graafisesti. Sirontakuvio kertoo, onko tarkasteltavien muuttujien suhde lineaarinen, eli kasvaako tai väheneekö toisen muuttujan arvo toisen muuttujan arvojen kasvaessa tai vähentyessä. Toisin sanoen sirontakuviosta nähdään helposti, onko korrelaatiotarkastelu mielekäs. Jotta muuttujien suhdetta voitaisiin kutsua lineaariseksi, arvojen ei tietenkään tarvitse asettua täsmälleen samalle suoralle. Näin olisi vain täydellisen positiivisen tai negatiivisen korrelaation tapauksessa (korrelaatiokerroin 1 tai -1).
Muuttujien välillä on lineaarinen yhteys:
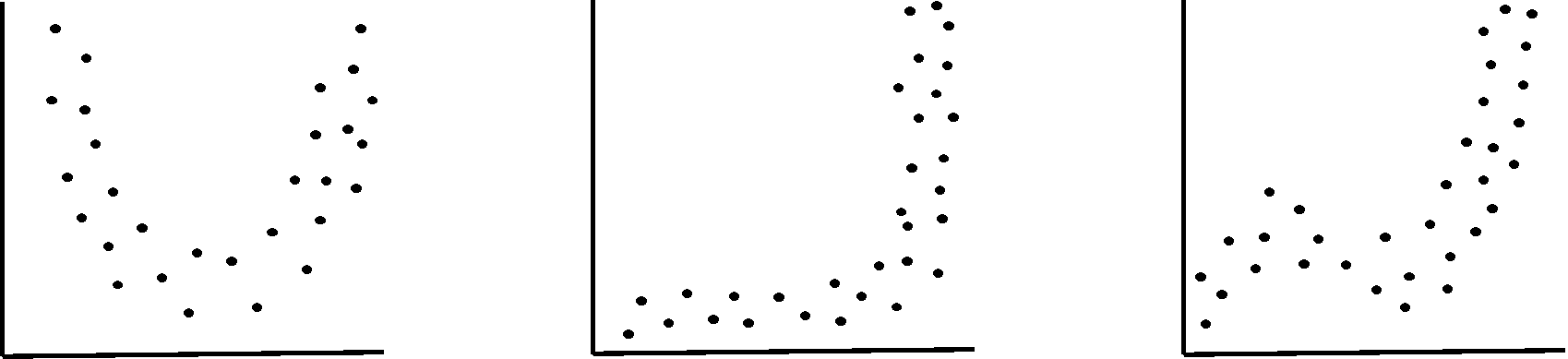
Muuttujien välillä on yhteys, mutta se ei ole lineaarinen:
Käytännössä korrelaatiokerroin on sen suoran kulmakerroin, joka on muuttujien välisen yhteyden kuvaamiseen sopivin. Sopivuus tarkoittaa sellaisen suoran kuvaamista, joka minimoi suoran arvojen ja havaintoaineiston arvojen välisen virheen, eli etäisyydet suorasta. Kulmakerroin voi olla joko negatiivinen tai positiivinen, tai yhteyden puuttuessa nolla. (Ks. myös regressioanalyysi).
Spearmanin korrelaatiokerroin

Järjestysasteikolliset muuttujat eivät täytä normaalijakautuneisuuden ja jatkuvuuden kriteerejä. Joskus myös aineistossa on runsaasti poikkeavia havaintoja eikä normaalijakautuneisuuden oletus täyty. Silloin Pearsonin korrelaatiokerrointa ei voi soveltaa aineistoon, koska se perustuu parametrisiin oletuksiin. Järjestysasteikollisille muuttujille on kuitenkin kehitetty epäparametrinen Spearmanin korrelaatiokerroin.
Spearmanin korrelaatiokerroin (Spearmanin Rho, ρ) mittaa sitä, kuinka samanlainen havaintojen järjestys on kahdella muuttujalla. Käytännössä kyse on siitä, että havainnot asetetaan suuruusjärjestykseen. Pienin havaintoarvo saa järjestysluvun 1, seuraavaksi pienin luvun 2 ja niin edelleen. Nämä voidaan merkitä seuraavasti:
Tämän jälkeen tarkastellaan kuinka paljon havaintoparin järjestysluvut poikkeavat toisistaan. Toiseen potenssiin korottamalla päästään eroon negatiivisista erotuksista (Nummenmaa 2004).
Koska Spearmanin korrelaatiokerroin perustuu järjestyslukuihin, positiivinen korrelaatiokerroin kertoo, että muuttujien arvojen järjestykset ovat samansuuntaiset, ja negatiivinen, että muuttujien arvojen järjestykset ovat erisuuntaiset. Järjestyslukujen täyttä samansuuntaisuutta kuvaisi korrelaatiokerroin 1, ja täyttä erisuuntaisuutta korrelaatiokerroin -1. Mikäli järjestyslukujen välillä ei olisi lainkaan yhteyttä, Spearmanin korrelaatiokerroin olisi nolla.
Osittaiskorrelaatio

Osittaiskorrelaatio on lineaarisen regressioanalyysin perusta. Osittaiskorrelaatiota käytetään useamman kuin kahden muuttujan yhteyksien selvittämiseen. Toisin sanoen osittaiskorrelaatiolla tutkitaan kahden muuttujan suhdetta ottamalla huomioon eli kontrolloimalla eli vakioimalla yhden tai useamman muuttujan vaikutus tähän suhteeseen. Mikäli kontrolloitavia muuttujia on enemmän kuin yksi, on suositeltavaa käyttää analyysiin osittaiskorrelaation sijasta monimuuttujaregressioanalyysia.
Osittaiskorrelaatiota laskettaessa molemmat muuttujat, joiden välisestä yhteydestä ollaan kiinnostuneita, voivat olla jatkuvia (esim. tenttipistemäärä ja luetut kirjat) ja toinen jatkuva ja toinen kategorinen.
Käytännössä osittaiskorrelaatio tarkoittaa sitä, että muuttujalla X ja Y on joko todellinen tai näennäinen yhteys, mutta kun otetaan huomioon muuttujan Z vaikutus, tämä yhteys muuttuu tai jopa häviää.
Useimmiten muuttujat X, Y ja Z korreloivat tutkimusasetelmissa ainakin jonkin verran keskenään. Silloin on tärkeää tutkia, mikä on muuttujan x vaikutus muuttujaan y, kun muuttujan z vaikutus poistetaan. Tällöin sama yhteisvaihtelu ei tule lasketuksi kahta kertaa ja saadaan x:n ja y:n "puhdas korrelaatio". Toisin sanoen x:n ja y:n korrelaatiosta poistetaan x:n ja z:n korrelaatio (Nummenmaa 2004). Voisimme olla kiinnostuneita esimerkiksi siitä, miten luettujen kirjojen lukumäärä korreloi tenttipistemäärän kanssa kun vastaajan opintopistemäärä on kontrolloitu. Oletuksena tässä on se, että opiskeltavan aineksen jäsentäminen paranee opintojen edetessä. Mikäli haluamme tarkastella vain luettujen kirjojen määrän "puhdasta" vaikutusta tenttipistemäärään, opintopistemäärä on siis kontrolloitava. Osittaiskorrelaatio voidaan laskea kun muuttujien x (luetut kirjat), y (tenttipistemäärä) ja z (opintopistemäärä) ovat tiedossa:
Korrelaatio ja kausaaliteetti

Kausaliteetti kuvaa kahden tapahtuman välistä syy–seuraus -suhdetta. Klassinen lause "korrelaatio ei tarkoita kausaalisuutta" tarkoittaa yksinkertaisesti sitä, että pelkän muuttujien yhteisvaihtelun perusteella emme voi määrittää niiden välisiä syy-seuraussuhteita tai ylipäätään osoittaa, että muuttujilla olisi yhteys reaalimaailmassa. Esimerkkejä on useita.
Klassinen esimerkki yhteyden häviämisestä on jäätelön myynnin, ilman lämpötilan ja lämpöhalvausten yhteys. Korrelaatiotarkastelussa voidaan havaita, että jäätelön myynnin lisääntyessä myös lämpöhalvausten esiintyvyys kasvaa. Kuitenkin kontrolloitaessa lämpötilan vaikutus, havaitaan, että lämpötilan kohoaminen lisää sekä jäätelön myyntiä että lämpöhalvausten esiintyvyyttä ja korrelaatiota alkuperäisten muuttujien välillä ei ole.
1 Korjattu 14.8.2023 esitetyssä arvossa ollut pilkkuvirhe. Aiemmin kohdassa luki "suurempi kuin 0.63".