Regressioanalyysi
Markus Kaakinen & Noora Ellonen (Viittausohje. Tämä on uudistettu versio Mikko Mattilan [2003] artikkelista Regressioanalyysi)
Tämä luku on jaettu 6 osaan ja pääset alla olevasta listasta siirtymään suoraan haluamaasi osaan.
Regressioanalyysin (engl. regression analysis) avulla tutkitaan yhden tai useamman selittävän muuttujan yhteyttä selitettävään muuttujaan. Sen avulla voidaan pyrkiä vastaamaan esimerkiksi siihen, onko koulutuksen pituus yhteydessä saadun palkan suuruuteen ja millainen tämä yhteys mahdollisesti on. Regressioanalyysin erityinen etu on, että siinä voidaan tutkia yhtä aikaa monen selittävän muuttujan yhteyttä selitettävään muuttujaan. Tällöin tulokset kertovat, mikä on yksittäisen selittävän muuttujan yhteys selitettävään muuttujaan, kun muut mallissa mukana olevat muuttujat on otettu huomioon.
Regressioanalyysi on monipuolinen ja joustava menetelmä muuttujien välisten suhteiden tutkimukseen. Sen edellytyksenä on, että selitettävä muuttuja on vähintään välimatka-asteikollinen (ks. muuttujien mittaustaso ja regressioanalyysin oletukset). Selittävät muuttujatkin ovat yleensä vähintään välimatka-asteikollisia, mutta myös luokittelu- ja järjestysasteikollisia muuttujia voidaan sisällyttää analyysiin. Tällöin niistä täytyy tehdä niin sanottuja dummy-muuttujia (ks. kategoristen muuttujien käyttö regressioanalyysissä).
Regressioanalyysin tulosten tulkintaan liittyy myös rajoituksia, jotka on syytä tunnistaa. Ehkä keskeisintä on muistaa, että regressioanalyysi kertoo muuttujien välisistä yhteyksistä. Tutkittavien ilmiöiden välisiä kausaalisuhteita ei voida osoittaa regressioyhtälön avulla, sillä syy-seuraussuhteiden tarkastelu vaatii aina erityisen tutkimusasetelman (ks. Kausaalipäättely havaintoaineistoon perustuvassa tutkimuksessa). Myös esimerkiksi kokeellisessa tutkimuksessa voidaan hyödyntää regressioanalyysia, mutta silloin kausaalipäätelmät perustuvat taustalla olevaan tutkimusasetelmaan eivätkä analyysimenetelmään. Regressiomallin rakentaminen ja tulosten tulkinta on hyvä perustaa teoriaan ja aikaisempaan tutkimukseen. Esimerkiksi selittävä ja selitettävä muuttuja valitaan teoreettisen ymmärryksen perusteella, sillä regressiomalli ei kerro vaikutussuhteen suuntaa (vaikuttaako muuttuja X muuttujaan Y vai toisin päin). Pitkittäisasetelmien avulla muuttujien välisten yhteyksien suuntaa on mahdollista analysoida tarkemmin.
Regressiosuora ja -kerroin

Regressioanalyysin perusperiaatteet voidaan esittää havainnollisesti kuvion 1 avulla. Hajontakuviossa on esitetty 15 valtion lukutaidottomuusprosentti ja valtion panostus koulutukseen prosenttiosuutena bruttokansantuotteesta. Jokainen kuvion piste viittaa yhteen maahan (havaintoon). Esimerkiksi Intiassa oli vuonna 1991 lukutaidottomia noin 48 % väestöstä ja maan bruttokansantuotteesta käytettiin 3,3 % koulutusmenoihin. Kannattaa huomata, että kuviossa esitetyt maat ja luvut ovat oikeita, mutta niiden valinta perustui tarkoituksenmukaisuusharkintaan. Näin esitetyt empiiriset tulokset ovat yleistettävyyden kannalta parhaimmassakin tapauksessa vain suuntaa-antavia.
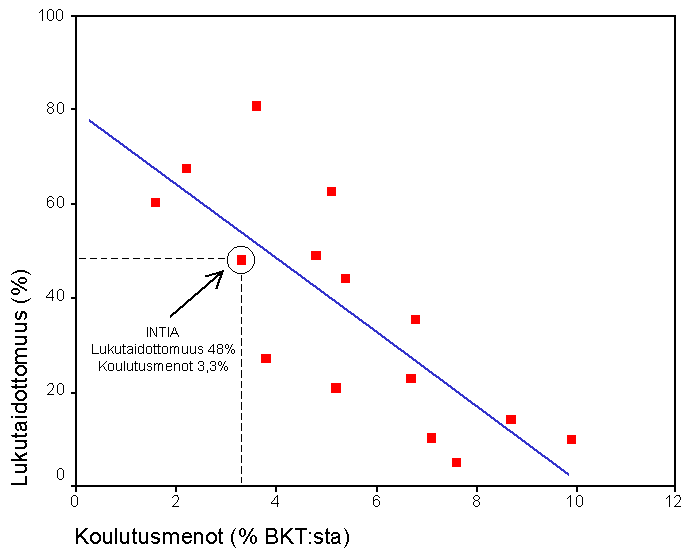
Kuviosta näkee selvästi, miten lukutaidottomuus ja panostus koulutukseen ovat yhteydessä toisiinsa. Mitä suurempi osuus maan bruttokansantuotteesta sijoitetaan koulutukseen, sitä vähemmän maassa on lukutaidottomia. Regressioanalyysin avulla voidaan tutkia sekä näiden kahden muuttujan välisen yhteyden suuntaa ja voimakkuutta että yhteyden tilastollista merkitsevyyttä. Yhteyden suunta kertoo sen, väheneekö (negatiivinen yhteys) vai kasvaako (positiivinen yhteys) lukutaidottomuus, kun koulutusmenojen osuus kasvaa. Yhteyden voimakkuus kertoo, kuinka paljon lukutaidottomuus muuttuu, kun koulutusmenojen osuus kasvaa yhdellä yksiköllä. Mitä suurempi muutos on, sitä vahvempi on muuttujien välinen yhteys.
Tilastollinen merkitsevyys puolestaan kertoo, kuinka todennäköisesti vastaava yhteys havaittaisiin, jos muuttujien välillä ei todellisuudessa olisi yhteyttä (ks. tilastollinen päättely ja hypoteesien testaus). Pieni todennäköisyys (p-arvo) siis kertoo, että vastaavan tuloksen saaminen olisi siinä tapauksessa epätodennäköistä. Tilastollisesti merkitsevän tuloksen kohdalla voidaan olettaa, että muuttujien välinen yhteys poikkeaa nollasta (valitulla luottamustasolla). Mikäli tulos perustuu edustavaan aineistoon, voidaan lisäksi olettaa, että yhteys on voimassa päättelyn kohteena olevassa perusjoukossa.
Kuvioon piirretty viiva on niin sanottu regressiosuora (regression line). Se osoittaa muuttujien välisen yhteyden suunnan ja voimakkuuden. Jos regressiosuora laskee alaspäin, on muuttujilla negatiivinen yhteys ja jos se nousee ylöspäin, on niillä positiivinen yhteys. Mitä lähempänä vaakatasoa suora on (tai mitä pienempi on sen kulmakertoimen itseisarvo), sitä heikompi yhteys muuttujien välillä on.
Regressiosuora voidaan merkitä kaavan avulla seuraavasti:
Kaavassa Y tarkoittaa selitettävän muuttujan arvoa, a on niin sanottu vakiotekijä, X on selittävän muuttujan arvo ja b on regressiokerroin (regression coefficient). Regressiokerroin on regressiosuoran kulmakerroin. Jos se saa negatiivisen arvon, on suora laskeva ja jos regressiokerroin on positiivinen, on suora nouseva. Jos regressiokerroin on nolla, ei muuttujien välillä ole lineaarista eli suoraviivaista yhteyttä. Vakiotekijä kertoo, minkä arvon selitettävä muuttuja saa silloin, kun selittävän muuttujan X arvo on nolla. Se siis kertoo, missä kohtaa regressiosuora leikkaa kuvion y-akselin.
Regressiokaava ei koskaan selitä täydellisesti Y:n vaihtelua. Regressiokaavan lopussa oleva ε viittaakin virhetermiin eli regressioyhtälön ennustaman vastemuuttujan arvon poikkeamiseen sen "todellisesta" arvosta. Virhetermiin sisältyvät kaikki sellaiset tekijät, jotka ovat yhteydessä selitettävän muuttujan vaihteluun, mutta eivät ole mukana mallissa. Osa tutkijoista on myös sitä mieltä, että ihmistieteissä virhetermi sisältää lisäksi tutkimuskohteeseen liittyvää aitoa satunnaisuutta. Virhetermi on siis väistämätön osa regressiomalleja, jos hyväksymme sen, ettei malli koskaan täysin selitä tietyn ilmiön vaihtelua.
Regressioanalyysin avulla voidaan selvittää kaavan vakiotekijän ja regressiokertoimen arvot. Esimerkiksi kuvion 1 aineiston perusteella saadaan seuraava regressioyhtälö:
Tässä yhtälössä lukutaidon todellinen arvo Y on korvattu sen ennustetulla arvolla Y’. Yhtälön regressiokerroin (eli b:n arvo) on -7,9. Regressiokerroin kertoo, kuinka monen yksikön verran selitettävän muuttujan ennustettu arvo muuttuu, kun selittävä muuttuja kasvaa yhden yksikön. Esitetty yhtälö voidaan tulkita seuraavasti. Kun koulutusmenoja lisätään yhdellä prosenttiyksiköllä bruttokansantuotteesta, vähenee lukutaidottomien määrä keskimäärin 7,9 prosenttiyksikköä. Vakiotekijä kertoo, kuinka paljon maassa olisi lukutaidottomia, jos koulutusmenot olisivat nolla eli maassa ei panostettaisi laisinkaan rahaa koulutukseen. Tällöin lukutaidottomia olisi maassa 80 %. Tämä on tietenkin vain hypoteettinen arvio, koska maailmasta tuskin löytyy sellaista maata, missä koulutukseen ei panostettaisi ollenkaan.
Yllä kuvatun regressiokertoimen rajoite on se, että se on sidottu selittävän muuttujan ja selitettävän muuttujan skaalaan. Mitä kapeampi on esimerkiksi selittävän muuttujan skaala, sitä suurempia ovat tyypillisesti regressiokertoimet. Näin kahden eriskaalaisen selittävän muuttujan regressiokertoimia ei voida suoraan verrata keskenään. Tästä syystä regressiokertoimen ohella raportoidaan usein standardoitu regressiokerroin (ks. muuttujien standardointi).
Standardoitu regressiokerroin kertoo sen, montako keskihajontaa (ja mihin suuntaan) selitettävän muuttujan arvo muuttuu, kun selittävä muuttuja kasvaa yhdellä keskihajonnalla. Standardoidun regressiokertoimen tulkinta muistuttaa korrelaatiokertoimen tulkintaa, ja sen avulla voidaan paremmin verrata kahden eriskaalaisen selittävän muuttujan yhteyttä vastemuuttujaan. Myös standardoidun regressiokertoimen tulkintaan liittyy rajoitteita. Vaikka kerroin ei ole sidottu muuttujien skaalaan, siihen vaikuttavat kuitenkin niiden hajonnat. Standardointi myös muuttaa muuttujat keinotekoiselle asteikolle. Näin tulokset eivät enää kerro esimerkiksi suoraan sitä, kuinka monta prosenttiyksikköä lukutaidottomuus muuttuu koulutusmenojen kasvaessa tietyn verran. Yhteiskuntatieteissä vastemuuttujalla ei kuitenkaan usein ole tällaista luonnollista asteikkoa, jolloin standardointi ei mutkista tulosten tulkintaa samalla tavalla.
Yksittäisen havainnon arvon etäisyyttä regressiosuorasta kutsutaan havainnon residuaaliksi (residual). Esimerkiksi kuviosta 1 tiedämme, että Intiassa lukutaidottomuuden taso on aineistossa 48 %. Regressioyhtälön avulla voidaan myös laskea regressiomallin ennuste Intian lukutaidottomuudelle. Se saadaan sijoittamalla regressiokaavaan selitettävän muuttujan eli koulutukseen menevien varojen bruttokansantuoteosuus, joka on Intian kohdalla 3,3. Näin saadaan regressiomallin ennusteeksi Intian osalta 53,9 (= 80 - 7,9 * 3,3) Tämä osoittaa, ettei regressiomalli ole täysin tarkka, sillä Intian lukutaidottomien havaittu osuus poikkeaa ennustetusta. Intian poikkeama (residuaali) mallissa on 48 - 53,9 = -5,9 . Residuaalin merkitys on lähellä yllä kuvattua regressioyhtälön virhetermiä (ennustetun arvon ja "todellisen" arvon välinen ero). Koska virhetermiä ei voida havaita, sen ominaisuuksia tarkastellaan usein residuaalien kautta (ks. regressioanalyysin oletukset).
Regressiomallin pätevyyttä voidaan arvioida sen mukaan, kuinka lähelle kuvion pisteet sijoittuvat regressiosuoraa. Mitä lähempänä suoraa ne sijaitsevat, sitä parempi on regressiomallin selitysaste ja päinvastoin. Jos mallilla on hyvä selitysaste, sen avulla voidaan hyvin tarkasti arvioida, mikä on esimerkiksi jonkin yksittäisen maan lukutaidottomuusprosentti silloin, kun tiedetään kuinka paljon maassa sijoitetaan resursseja koulutukseen. Mitä kauempana pisteet suorasta sijaitsevat, sitä epävarmempia ovat ennusteet
Regressiomallin selitysvoimaa voidaan tarkastella laskemalla yhteen kaikkien havaittujen arvojen poikkeama regressiomallin ennustamista arvoista. Koska osa poikkeamista on positiivisia (havainnot sijoittuvat regressiosuoran yläpuolelle) ja osa negatiivisia (havainnot sijoittuvat regressioviivan alapuolelle), tulee poikkeamat kohottaa neliöiksi (toiseen potenssiin) ennen yhteen laskemista. Näin suurempi yhteen laskettu arvo kertoo aina suuremmista poikkeamista. Lineaarisessa regressioanalyysissa useimmin käytetty pienimmän neliösumman estimointimenetelmä (ordinary least squares, OLS) perustuukin siihen, että mallin lopulliset kertoimet tuottavat pienimmän mahdollisen residuaalien neliösumman. Käytännössä regressiomallien selitysaste raportoidaan yleensä niin sanotulla R2-kertoimella tai sen korjatulla versiolla.
Regressioanalyysin tulosten tulkinta

Seuraavaksi käytetään Maailmanpankin väestötilastoaineistoa regressioanalyysin tulosten esittelemiseksi. Selitettävänä muuttujana on maakohtainen suhteellinen kuolleisuus vuonna 2017 (eli paljonko kuolleita on 1000 henkilöä kohden). Selittävänä muuttujana mallissa on HI-viruksen esiintyvyys väestössä (viruksen kantajien %-osuus 15–49-vuotiaassa väestössä). Aineistossa on yhteensä 264 maata, maaryhmää ja muuta aluetta. Kuolleisuus näissä vaihtelee 1,2 ja 15,5 välillä (kuollutta 1000 henkilöä kohden vuodessa). Seuraavaksi tarkastellaan yhden muuttujan regressiomallin avulla HI-viruksen esiintyvyyden ja kuolleisuuden välistä yhteyttä (ks. SPSS-harjoitus 1).
Taulukossa 1 on esitetty regressioanalyysin tulokset. Taulukon yläosassa ovat analyysin selittävät muuttujat, niiden regressiokertoimet, standardoidut regressiokertoimet, t-arvot ja p-arvot. Taulukon alaosa sisältää regressiomallin pätevyyden arviointiin sopivia tunnuslukuja.
| B | Keskivirhe | Beta | t | p-arvo | |
| Vakio | 7,63 | 0,24 | 33,84 | 0,000 | |
| HI-viruksen esiintyvyys (%) | 0,09 | 0,05 | 0,16 | 1,99 | 0,048 |
| R2 | 0,03 | ||||
| Korjattu R2 | 0,02 | ||||
| F-testi |
3,97
p-arvo = 0,048 |
||||
| Estimaatin keskivirhe | 2,45 |
Ennen regressiokertoimien varsinaista tulkintaa kannattaa kiinnittää huomiota niiden tilastolliseen merkitsevyyteen. Regressioanalyysin yhteydessä testataan jokaisen selittävän muuttujan osalta, ovatko ne yhteydessä selitettävään muuttujaan eli eroavatko niiden regressiokertoimet tilastollisesti merkitsevästi nollasta (ks. tilastollinen päättely ja hypoteesien testaus). Tällaiseen tarkoitukseen sopiva testimenetelmä on niin sanottu t-testi. Testiä varten jokaiselle selittävälle muuttujalle lasketaan t-arvo, jonka suuruus (suhteessa mallin vapausasteiden määrittämään t-jakaumaan) ratkaisee sen, voidaanko muuttujan kerrointa pitää tilastollisesti merkitsevänä. Yleisesti käytetyn 95 %:n luottamustason mukaan p-arvot, jotka ovat pienempiä kuin 0,05, katsotaan tilastollisesti merkitseviksi. Taulukon viimeisessä sarakkeessa on esitetty regressiokertoimien t-testiin perustuvat p-arvot. Ne osoittavat, että sekä vakiotermi että HIV-tapausten laajuuden regressiokerroin eroavat tilastollisesti nollasta. Kaikki regressioanalyysiin sopivat ohjelmat tuottavat nämä tunnusluvut automaattisesti.
Taulukon 1 tulokset siis osoittavat, että HI-viruksen esiintyvyyden ja maan suhteellisen kuolleisuuden välillä on positiivinen yhteys (regressiokertoimen etumerkki on positiivinen). Kerroin on arvoltaan 0,09 mikä tarkoittaa sitä, että HIV-tartunnan saaneiden suhteellisen osuuden kasvu yhdestä prosentista kahteen lisää kuolleisuutta 0,09 yksikköä. Yhteys on myös tilastollisesti merkitsevä 95 %:n luottamustasolla (p = 0,048).
Taulukon 1 alalaidassa on esitetty tärkeimmät regressioanalyysin selitysvoimaa kuvaavat testit. Tällaisia testejä on useita, mutta R2-luku ja F-testi ovat yleisemmin käytetyt. R2-luku on regressiomallin selitysosuus. Se kertoo kuinka suuren prosenttiosuuden selitettävän muuttujan vaihtelusta regressionanalyysin selittävät muuttujat pystyvät selittämään. R2-luku vaihtelee nollan ja yhden välillä. Se saadaan laskemalla selitettävän muuttujan arvojen ja mallin tuottamien ennustearvojen korrelaation neliö. Jos R2-luku on pieni regression selittävät muuttujan pystyvät selittämään vain vähän selitettävän muuttujan vaihtelusta ja päinvastoin.
Taulukossa 1 R2-luku on 0,03. Tämä tarkoittaa, että HI-viruksen esiintyvyydellä pystytään selittämään maiden välistä kuolleisuuden vaihtelua suhteellisen heikosti: 3 % kuolleisuudesta on selitettävissä HI-viruksen esiintyvyydellä. On kuitenkin huomattava, että selitysosuutta kuvaavat luvut ovat merkityksellisiä aina jonkin tietyn regressiomallin asettamassa kontekstissa. Jos kuolleisuutta selitettäisiin lisäksi muilla siihen vaikuttavilla tekijöillä, HI-viruksen esiintyvyyden selitysosuus olisi luultavasti pienempi.
Korjattua R2-lukua (adjusted R2) käytetään silloin, kun halutaan verrata kahden regressioanalyysin tuloksia keskenään. Korjattu R2-luku ottaa huomioon mallin sisältämien selittävien muuttujien lukumäärän. Se on arvoltaan aina pienempi tai yhtä suuri kuin varsinainen R2-luku. Korjaus R2-lukuun tarvitaan sen vuoksi, että uusien selittävien muuttujien lisääminen regressioanalyysiin nostaa aina R2-lukua, vaikka nämä lisätyt muuttujat eivät todellisuudessa pystyisikään lisäämään selityskykyä. Silloin kun tarkasteltavana on vain yksi regressiomalli, ei korjatun R2-luvun käyttäminen ole tarpeellista, mutta regressiomalleja verratessa siitä on hyötyä. Jatkossa taulukon 1 regressioanalyysia laajennetaan uusilla muuttujilla. Siksi korjattu R2-luku on raportoitu myös tässä yhteydessä, jotta vertaileminen myöhemmin esitettyihin laajennettuihin regressiomalleihin on mahdollista.
F-testi on tilastollinen testi, joka kertoo, pystytäänkö regressioanalyysissa olevilla muuttujilla ylipäänsä selittämään selitettävän muuttujan vaihtelua. Koska se on tilastollinen testi, sen tuottamaa p-arvoa tulkitaan suhteessa valittuun luottamustasoon. Taulukossa 1 F-testin tulos on tilastollisesti merkitsevä. Tämä ei sinänsä ole yllätys, koska myös selittävän muuttujan regressiokerroin on tilastollisesti merkitsevä. On kuitenkin mahdollista, että yhdenkään selittävän muuttujan regressiokerroin ei ole tilastollisesti merkitsevä, mutta F-testin tulos on. Tämä tarkoittaa sitä, että regressioanalyysin muuttujat pystyvät yhdessä selittämään selitettävän muuttujan vaihtelua, vaikka yksittäin katsoen ne eivät ole tilastollisesti merkitseviä. Tällaiset tapaukset ovat kuitenkin harvinaisia.
Viimeinen regressiomallin onnistuneisuutta kuvaava tunnusluku on estimaatin keskivirhe (standard error of the estimate). Tämä luku ilmoittaa regressiomallin residuaalien keskihajonnan (ks. hajontaluvut). Mitä suurempi se on, sitä suurempi on residuaalien hajonta ja samalla sitä pienempi mallin tarkkuus (selitysvoima). Estimaatin keskivirheen suuruus riippuu aina regressiomallin selitysvoiman lisäksi selitettävän muuttujan mittaluokasta. Taulukossa 1 se on 2,45, mikä on kohtalaisen suuri luku, kun se suhteutetaan kuolleisuuden vaihteluväliin (1,2–15,5). Tämä osoittaa, että HI-viruksen esiintyvyydellä tietyssä maassa ei pystytä kovinkaan tarkasti ennustamaan maan suhteellista kuolleisuutta.
Kategoristen muuttujien käyttö regressioanalyysissä

Edellisessä esimerkissä selittävä muuttuja (HI-viruksen esiintyvyys) oli jatkuva. Regressioanalyysissa voidaan kuitenkin käyttää myös kategorisia (luokittelu- tai järjestysasteikollisia) selittäviä muuttujia. Useampiluokkaiset muuttujat tulee kuitenkin muuttaa dummy-muuttujiksi ennen malliin lisäämistä. Dummy-muuttujaksi kutsutaan muuttujaa, joka voi saada vain kaksi eri arvoa (nolla ja yksi). Tällaiset muuttujat voivat ilmaista esimerkiksi, onko vastaaja opiskelija vai ei, asuuko vastaaja Porissa vai ei, tai onko tarkasteltu maa liittovaltio vai ei.
Oletetaan esimerkiksi, että afrikkalaisissa maissa elinajan odote on alhaisempi kuin muissa maissa. Tätä hypoteesia voi tutkia lisäämällä regressioanalyysiin dummy-muuttujan, joka saa arvon yksi silloin kun maa sijaitsee Afrikassa ja muutoin arvoksi tulee nolla.
Dummy-muuttujien regressiokertoimien tulkinta on erittäin yksinkertaista. Kerroin ilmoittaa, kuinka muuttujalla arvon yksi saava havaintoryhmä eroaa niistä havainnoista, jotka saavat arvon nolla. Jos kerroin on positiivinen, se ilmaisee kuinka paljon suurempi elinajan odote on Afrikassa kuin Afrikan ulkopuolisissa maissa. Jos se on negatiivinen, kertoo se kuinka paljon lyhyempi elinikä Afrikassa on.
Dummy-muuttujia voidaan käyttää myös tilanteessa, jossa laatu- tai järjestysasteikon muuttuja saa useampia kuin kaksi vaihtoehtoa. Tällaisessa tilanteessa yleinen periaate on, että uusia dummy-muuttujia täytyy luoda yksi vähemmän kuin laatu- tai järjestysasteikon muuttujassa on vastausvaihtoehtoja. Jos malliin tuodaan kaikki alkuperäisen muuttujan luokat, mallinnuksessa syntyy multikollineaarisuusongelma (yleensä ohjelmistot ratkaisevat tämä pudottamalla yhden luokan analyysista pois). Jos esimerkiksi laatueroasteikon muuttuja voi saada neljä eri arvoa, täytyy regressioanalyysia varten luoda kolme uutta dummy-muuttujaa. Analyysista pois jäävä luokka on niin sanottu referenssikategoria (ks. dummy-muuttujien tulkinta alla).
Dummy-muuttujien tulkinta
Oletetaan, että tutkija haluaa regressioanalyysin avulla selvittää henkilöiden iän ja koulutuksen vaikutusta heidän palkkatasoonsa. Tässä kuvitteellisessa esimerkissä koulutus on mitattu kolmiasteisella mittarilla, jonka vaihtoehdot ovat perusasteen koulutus, toisen asteen koulutus ja korkeakouluasteen koulutus. Regressioanalyysin tarpeisiin tästä muuttujasta täytyy luoda kaksi uutta dummy-muuttujaa. Ensimmäinen muuttuja voisi olla perusaste-muuttuja, joka saa arvon yksi, jos vastaajan korkein suorittama tutkinto on perusasteen koulutus. Muutoin muuttuja saa arvon nolla. Toinen muuttuja olisi toinen aste -muuttuja. Se saa arvon yksi, jos vastaajan korkein suorittama tutkinto on toisen koulutus. Muussa tapauksessa muuttuja muuttuja saa arvon nolla. Regressiomallissa selitettävänä muuttujana on vastaajan palkan suuruus euroina ja selittävinä muuttujina vastaajan kaksi edellä mainittua dummy-muuttujaa.
Useamman dummy-muuttujan tapauksessa regressiokertoimia tulee tulkita suhteessa valittuun referenssikategoriaan (pois jätettyyn luokkaan). Oletetaan, että tämän kuvitteellisen regressioanalyysin tuloksissa perusaste-muuttujan regressiokerroin on -1000 ja toinen aste-muuttujan -500. Nämä kertoimet tarkoittaisivat, että perustason tutkinnon suorittaneiden kuukausipalkka olisi keskimäärin tuhat euroa pienempi kuin korkeakoulututkinnon suorittaneiden ansiot. Toisen asteen tutkinnon suorittaneiden keskimääräinen kuukausipalkka taas olisi 500 euroa pienempi kuin korkeakoulututkinnon suorittaneiden palkka. Dummy-muuttujien regressiokertoimet ilmoittavat siis ryhmän keskimääräisen poikkeaman siitä ryhmästä, jolle ei tuotu malliin omaa dummy-muuttujaa.
Referenssikategorian valinta siis vaikuttaa tulosten tulkintaan. Analyysissa tarkastellaan pohjimmiltaan samoja ryhmiä, mutta vertailukohta riippuu referenssikategoriasta. Jos edelliseen regressiomalliin olisi lisätty perusaste- ja korkeakouluaste-muuttujat (jolloin toinen aste jäisi referenssikategoriaksi), olisivat niiden regressiokertoimet olleet -500 ja +500. Kertoimien mukaisesti perusasteen tutkinnon suorittaneiden kuukausipalkka olisi tässä kuvitteellisessa esimerkissä 500 euroa pienempi kuin toisen asteen tutkinnon suorittaneiden palkka. Korkeakoulututkinnon suorittaneiden keskimääräinen kuukausipalkka taas olisi 500 euroa suurempi kuin toisen asteen tutkinnon suorittaneilla. Tämä analyysi ei siis suoraan vertaa korkeakoulututkinnon ja perusteen tutkinnon suorittaneiden palkkaeroa (tai sen tilastollista merkitsevyyttä), vaikka se onkin kertoimista pääteltävissä. Tutkimuksessa referenssikategoria kannattaa siis valita niin, että jotain teoreettisesti kiinnostavaa ryhmää verrataan muihin.
Usean muuttujan regressioanalyysi

Edellisissä regressioanalyysin esimerkeissä oli vain yksi selittävä muuttuja. Regressioanalyysin etu on kuitenkin se, että siihen voidaan sisällyttää useita selittäviä muuttujia yhtäaikaisesti. Tällöin muuttujien regressiokertoimet kertovat, kuinka paljon selitettävän muuttujan arvo muuttuu, kun selittävän muuttujan arvo kasvaa yhdellä yksiköllä ja kaikkien muiden muuttujien arvo pysyy vakiona. Toisin sanoen usean muuttujan regressioanalyysissa regressiokertoimet ilmoittavat selittävän muuttujan vaikutuksen selitettävään muuttujaan niin, että muiden mallin muuttujien vaikutus on vakioitu.
Tällainen muiden tekijöiden vakiointi (tai tilastollinen kontrollointi) on havaintotutkimuksessa tai muussa kuin satunnaistamiseen perustuvissa tutkimuksissa hyvin tärkeää. Näin huomioidaan se mahdollisuus, että kahden analysoitavan muuttujan välillä havaittu yhteys selittyy todellisuudessa jollain kolmannella tekijällä. Tarkemmin sanottuna regressioanalyysissa tulee vakioida sellaiset tekijät, joiden voidaan olettaa olevan yhteydessä sekä selittävään muuttujaan että selitettävään muuttujaan. Jos tällaisia olennaisia tekijöitä ei vakioida, ovat regressiomallin tulokset epäluotettavia.
Jos esimerkiksi analysoimme koulutuksen ja koetun hyvinvoinnin välistä yhteyttä, tulisi mallissa todennäköisesti olla mukana myös vastaajan tulot. Korkeammin koulutetut henkilöt ovat keskimäärin parempituloisia, ja tulot puolestaan ovat yhteydessä koettuun hyvinvointiin. Jos tulot jätettäisiin mallista pois, todellisuudessa toimeentulosta johtuva osa koetun hyvinvoinnin vaihtelusta näyttäisi regressiomallissa virheellisesti selittyvän koulutuksella. Koulutuksen regressiokertoimeen eivät kuitenkaan vaikuta sellaiset mallista puuttuvat muuttujat, jotka korreloivat vain koetun hyvinvoinnin kanssa, mutta eivät ole yhteydessä koulutukseen.
Mallin rakentamisessa onkin hyvin tärkeää harkita, mitä muuttujia otetaan mukaan ja mitä jätetään pois. Lähtökohtaisesti kaikkien olennaisten muuttujien tulisi olla mukana mallissa. Toisaalta liian monen muuttujan sisällyttäminen malliin on myös ongelmallista. Esimerkiksi muiden selittäjien kanssa vahvasti korreloivat muuttujat lisäävät muiden muuttujien kertoimien vaihtelua. Ääritapauksessa liian monen vastemuuttujan lisääminen voi saada aikaan täydellisen multikollineaarisuuden. Muuttujien lisääminen kuluttaa aina myös mallin vapausasteita. Malliin valittavien muuttujien määrää on siis pakko rajata. Yleensä malliin rajattavien muuttujien valinta kannattaa tehdä teorian ja aikaisemman kirjallisuuden perusteella.
Kahden selittävän muuttujan regressioanalyysin kaava voidaan esittää seuraavasti:
Kaavassa Y' \(Y'\) on selitettävän muuttujan ennustettu arvo, a \(a\) vakiotekijä, X1 ja X2 \( X_1 \) ja \( X_2 \) ja selittävät muuttujat sekä b1 ja b2 \( b_1 \) ja \( b_2 \)niiden regressiokertoimet.
Seuraavaksi jatkamme suhteellisen kuolleisuuden selittämistä HI-viruksen esiintyvyydellä lisäämällä regressioanalyysiin uusina muuttujina terveydenhuoltomenot (% maan BKT: sta), imeväiskuolleisuuden (kuolleita/1000 syntynyttä kohden), syntyvyyden (syntyneitä/1000 henkilöä kohden) ja bruttokansantulon (BKTL) (ks. useamman muuttujan regressioanalyysista SPSS-harjoituksessa 1). Imeväiskuolleisuus vaihtelee 1,6 ja 85,9 välillä ja syntyvyys vaihtelee 6,7 ja 46,5 syntyneen välillä. Terveydenhuoltomenojen osuus BKT: sta vaihtelee 1,6 ja 17,7 prosentin välillä.
Aineistossa bruttokansantuloa tarkasteleva muuttuja perustuu Maailmanpankin jaotteluun matalan, alemman keskitason, ylemmän keskitason ja korkean bruttokansantulon maihin. Todellisuudessa bruttokansantuloa kannattaisi todennäköisesti tarkastella analyysissä jatkuvana muuttujana. Tässä esimerkissä käsittelemme sitä kuitenkin kategorisena muuttujana harjoitellaksemme dummy-muuttujan käyttöä lineaarisessa regressioanalyysissä. Muuttujasta muodostettiin neljä dummy-muuttujaa: matala BKTL (kyllä/ei), alemman keskitason BKTL (kyllä/ei), ylemmän keskitason BKTL (kyllä/ei) ja korkea BKTL (kyllä/ei). Koska kaikkia neljää dummy-muuttujaa ei voida lisätä samaan malliin (katso Dummy-muuttujat yllä), tulee yksi niistä valita referenssikategoriaksi, ja jättää mallista pois. Tässä esimerkissä referenssikategoriaksi valitaan matala BKTL. Malliin lisättävien alemman keskitason BKTL:n, ylemmän keskitason BKTL:n ja korkean BKTL:N regressiokertoimet siis ilmaisevat sen, miten näiden ryhmien kuolleisuus eroaa matalan BKTL:n ryhmästä.
Myös HI-virustartunnan saaneiden osuutta kuvaava muuttuja luokiteltiin uudelleen tätä esimerkkiä varten. Siitä tehtiin niin ikään kaksiluokkainen dummy-muuttuja, joka kertoo, onko HI-virustartunnan saaneiden osuus maan väestöstä matala (0) vai korkea (1). Leikkauspisteenä käytettiin yhtä prosenttia 15–49-vuotiaasta väestöstä (0–0,99 % = matala, vähintään 1 % = korkea). Seuraavaksi tarkastellaan, onko HI-virustartuntojen määrä yhteydessä väestön kuolleisuuteen, kun syntyvyys, imeväiskuolleisuus, terveydenhoitomenot ja valtion bruttokansantulo on huomioitu.
Taulukossa 2 on esitetty tämän regressioanalyysin tulokset. HI-viruksen esiintyvyyden yhteys kuolleisuuteen säilyy, vaikka malliin lisättiin myös muita selittäviä muuttujia. Korkean HI-viruksen esiintyvyyden maissa kuolleisuus tuhatta henkilöä kohden on 1,14 henkilöä suurempi kuin matalan esiintyvyyden maissa (p = 0,04), kun muut mallissa olevat muuttujat on otettu huomioon.
Mallin muita muuttujia tarkastellessa havaitaan, että esimerkiksi syntyvyyden ja kuolleisuuden välinen yhteys on negatiivinen (B = -0,25). Yhteys on tilastollisesti erittäin merkitsevä (p < 0,001). Mitä enemmän maassa siis syntyy lapsia tuhatta henkeä kohden, sitä vähemmän maassa on vuosittain kuolemia suhteessa tuhanteen ihmiseen. Bruttokansantuloa tarkasteltaessa alemman keskitason, ylemmän keskitason ja korkean BKTL:n maaryhmiä tulee verrata matalan BKTL:n ryhmään (mallista puuttuva referenssikategoria). Näin ollen esimerkiksi korkean BKTL-tason maissa kuolleisuus on pienempää (-0,26) kuin matalan BKTL:n maissa, mutta ero ei ole tilastollisesti merkitsevä (p = 0,807). Myös muiden alemman keskitason ja ylemmän keskitason maissa kuolleisuus on vähäisempää kuin matalan BKT:n maissa, mutta nämäkään erot eivät ole tilastollisesti merkitseviä (ks. Taulukko 2).
| B | Keskivirhe | Beta | t | p-arvo | 95 % luottamustason luottamusväli | ||
| Vakio | 10,711 | 1,59 | 6,74 | 0,000 | 7,56 | 13,86 | |
| Syntyvyys (/1000 henk) | -0,25 | 0,05 | -0,97 | -5,18 | 0,000 | -0,35 | -0,15 |
| Imeväiskuolleisuus (/1000 synt.) | 0,10 | 0,02 | 0,85 | 5,03 | 0,000 | 0,06 | 0,14 |
| Terveydenhuoltomenot (% BKT:sta) | 0,05 | 0,09 | 0,05 | 0,59 | 0,558 | -0,13 | 0,24 |
| BKTL, alempi keskitaso | -0,81 | 0,69 | -0,14 | -1,17 | 0,245 | -2,18 | 0,56 |
| BKTL, ylempi keskitaso | -1,05 | 0,85 | -0,18 | -1,24 | 0,217 | -2,72 | 0,63 |
| BKTL, korkea | -0,26 | 1,06 | -0,04 | -0,25 | 0,807 | -2,35 | 1,83 |
| HI-viruksen esiintyvyys | 1,14 | 0,55 | 0,21 | 2,07 | 0,040 | 0,05 | 2,23 |
| R2 | 0,31 | ||||||
| Korjattu R2 | 0,27 | ||||||
| F-testi |
6,96
p-arvo = 0,000 |
||||||
| Estimaatin keskivirhe | 2,26 | ||||||
Taulukon 2 korjattu R2-luku luku osoittaa, että muiden selittävien muuttujien lisääminen regressiomalliin paransi mallin selityskykyä huomattavasti verrattuna Taulukon 1 tuloksiin. Taulukossa 1 korjattu R2-luku on 0,02 ja taulukossa 2 vastaava tunnusluku on 0,27. Lisäksi estimaatin keskivirhe on pienempi Taulukossa 2 (2,26) kuin Taulukossa 1 (2,45). Nämä molemmat tunnusluvut kertovat, että muiden muuttujien lisäämisen jälkeen eri maiden kuolleisuutta pystyttiin ennustamaan huomattavasti paremmin (mallin selitysaste nousi).