Regressiomallin arviointi
Markus Kaakinen & Noora Ellonen (Viittausohje. Tämä on uudistettu versio Mikko Mattilan [2003] artikkelista Regressioanalyysi)
Tämä on neljäs osa regressioanalyysista kertovassa luvusta ja pääset alla olevasta listasta siirtymään suoraan muihin luvun osiin.
Edellä esitettyjen regressioanalyysin oletusten tarkastelu on olennainen osa analyysin toteutusta, jotta saadut tulokset olisivat luotettavia. Regressiomallin oletukset koskevat varsinaisesti regressioyhtälön virhetermiä, jota ei voida havaita. Mallin virhetermiin liittyviä oletuksia on kuitenkin mahdollista arvioida mallien residuaalien avulla. Esimerkiksi muuttujien välisen yhteyden lineaarisuutta sekä virhetermin homoskedastisuutta ja normaalijakautuneisuutta tarkastellaan analysoimalla mallin residuaalien jakaumaa.
Sen lisäksi, että oletuksia tulee tarkastella analyysin edetessä, mallin arviointi ja mahdollisten ongelmien tunnistaminen kuuluu olennaisena osana regressioanalyysin raportointiin. Näin myös lukija voi arvioida esitettyjen tulosten luotettavuutta.
Seuraavaksi käsittelemme tiiviisti regressiomallin poikkeavien havaintojen ja multikollineaarisuuden arvioimisen pariaatteita. Sen jälkeen käsittelemme muuttujien välisten yhteyksien lineaarisuuteen ja virhetermin homoskedastisuuteen ja normaalijakautuneisuuteen liittyvien oletusten tarkastelua. Tässä artikkelissa keskitymme mallien arvioinnin perusperiaatteisiin, mutta regressiomallintamisesta kiinnostuneille on tarjolla myös perusteellisempia esityksiä mallien arvioinnista ja sen toteuttamisesta esimerkiksi SPSS-ohjelmistolla (esim. Darlington & Hayes 2017).
Poikkeavat havainnot eli outlier-tapaukset

Joskus yksittäisillä poikkeavilla havainnoilla voi olla suuri vaikutus regressioanalyysiin tuloksiin. Tällaisia havaintoja kutsutaan niiden englanninkielisen nimen mukaan outlier-tapauksiksi. Asia on havainnollistettu kuviossa 3. Kuvion oikeassa ylälaidassa oleva havainto on outlier-tapaus. Jos se poistetaan kuviosta, x- ja y-muuttujilla ei ole laisinkaan lineaarista riippuvuutta toisistaan.
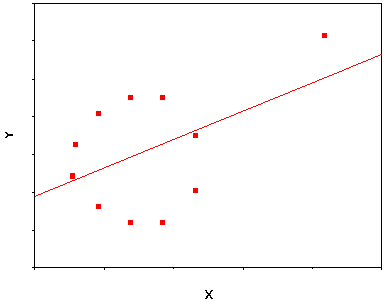
Joskus poikkeavien havaintojen taustalla voi olla yksinkertaisesti koodausvirhe, joka voidaan helposti korjata. Useimmiten kyse on kuitenkin siitä, että jokin tai jotkut havainnot saavat todellisuudessa muista huomattavasti poikkeavia arvoja. Tällaisessa tilanteessa kannattaa pohtia, mikä tekijä aiheuttaa havainnon poikkeavuuden. Jos sille löytyy mitattavissa oleva selitys, voidaan tämä tekijä sisällyttää analyysiin uutena muuttujana, jolloin se ei enää vääristä analyysin tuloksia. Jossain tapauksissa poikkeavat havainnot on mahdollista poistaa aineistosta, mutta se ei ole ongelmatonta. Tutkijan tulee perustella valintansa ja pohtia, miten poistaminen vaikuttaa tutkimustuloksiin tai niistä tehtäviin päätelmiin. Edustavatko poikkeavat havainnot esimerkiksi jotain ryhmää, joka ei enää ole analyysissa edustettuna? Poikkeavien havaintojen löytämiseksi on kehitetty erilaisia tunnuslukuja (esimerkiksi Mahalanobisin ja Cookin etäisyysmittarit). Näistä luvuista ja niiden tulkinnasta löytyy tietoa lisätietoja-kohdassa suositelluista kirjoista (ks. esim. Tabachnick ja Fidell 2013).
Multikollineaarisuus

Regressiomalliin on mahdollista lisätä useita keskenään korreloivia selittäviä muuttujia. Tässä tapauksessa muuttujien yhteinen varianssi otetaan mallissa huomioon (vakioidaan). Joskus selittävien muuttujien keskinäinen korrelaatio voi kuitenkin olla niin suuri, että se alkaa aiheuttaa ongelmia. Tällaista tilannetta kutsutaan multikollineaarisuudeksi. Regressioanalyysin oletukset koskevat täydellistä multikollineaarisuutta, mutta myös tätä vähäisempi multikollineaarisuus voi aiheuttaa ongelmia mallinnuksessa. Yleensä multikollineaarisuusongelmia ei synny, jollei selittävien muuttujien välillä ole todella suuria riippuvuuksia (esimerkiksi korrelaatiokerroin yli 0,9).
Pelkkä selittävien muuttujien välisten korrelaatiokertoimien tarkastelu ei kuitenkaan kuvaa riittävästi mahdollisia multikollineaarisuusongelmia. Olennaista on se, missä määrin kunkin selittävän muuttujan vaihtelu on kuvattavissa kaikkien muiden mallissa olevien selittävien muuttujien avulla. Multikollineaarisuusongelmia ilmenee, jos mallissa olevat muut muuttujat selittävät tietyn selitettävän muuttujan vaihtelun lähes täysin. Tässä tapauksessa kyseisen muuttujan regressiokertoimen keskivirheet kasvavat vääristyneen suuriksi, eikä siitä voida tehdä luotettavia tilastollisia päätelmiä (merkitseviä tuloksia on vaikea havaita).
Multikollineaarisuuden tarkasteluun voidaan käyttää esimerkiksi niin sanottua VIF-kerrointa (engl. variance inflation factor), jonka useimmat tilasto-ohjelmistot tulostavat regressiomallien yhteydessä. VIF-kertoimen neliöjuuri kertoo sen, kuinka moninkertaiseksi muuttujan keskivirheet kasvavat multikollineaarisuus-ongelmasta johtuen. VIF-kertoimelle ei ole olemassa yksiselitteistä raja-arvoa, joka kertoisi, milloin multikollineaarisuus on ongelmallista. Yhden yleisesti käytetyn peukalosäännön mukaan ongelmia esiintyy, jos VIF-kertoimen arvo on 10 tai enemmän (Keith, 2015). Tämä arvo on kuitenkin verrattain korkea ja usein käytössä on konservatiivisempi kynnysarvo (esimerkiksi 5–6). Olennaista on, että tutkija tuo esiin ja perustelee tarkastelussa käyttämänsä kynnysarvon. Argumentaatio on hyvä perustaa luotettavaan lähteeseen. Ongelmaa voi myös lähestyä sen kautta, missä määrin multikollineaarisuus vaikuttaa selittävän muuttujan keskivirheeseen. Jos VIF-kerroin on esimerkiksi kuusi, muuttujan keskivirheet ovat ongelmasta johtuen noin 2,5-kertaiset (kuuden neliöjuuri).
Moderaation tarkastelun yhteydessä taulukossa 3 on raportoitu esimerkissä käytetyn regressioanalyysin muuttujien VIF-arvot, jotka vaihtelevat välillä 1,33–6,83. Useimpien muuttujien kohdalla ei siis havaita korkeaa multikollineaarisuutta. Syntyvyyden kohdalla (VIF-kerroin = 6,83) korrelaatio muiden muuttujien välillä on kuitenkin korkeampaa. Yleensä tässä kohtaa voisi olla syytä selvittää tarkemmin, minkä muuttujien kanssa syntyvyys korreloi. Ongelmaa voisi yrittää ratkaista esimerkiksi muuttujamuunnosten avulla. Moderaatiomalleissa multikollineaarisuus liittyy usein siihen, että alkuperäisen muuttujat korreloivat voimakkaasti interaktiotermin kanssa. Tästäkin syystä muuttujat kannattaa standardoida tai ainakin keskittää ennen interaktiotermin lisäämistä.
Lineaarisuusoletus

Regressioanalyysin avulla tutkitaan lähtökohtaisesti muuttujien välisiä lineaarisia eli suoraviivaisia yhteyksiä. Joissain tapauksissa muuttujien välinen yhteys voi kuitenkin olla luonteeltaan epälineaarinen, jolloin se ei ole kuvattavissa lineaarisen mallin avulla. Toisin sanoen tutkija yrittää sovittaa aineistoon sellaista yhteyttä, joka istuu siihen huonosti. Kuviossa 4 on esitetty kaksi tilannetta, joissa x- ja y-muuttujien välillä on epälineaarinen yhteys.
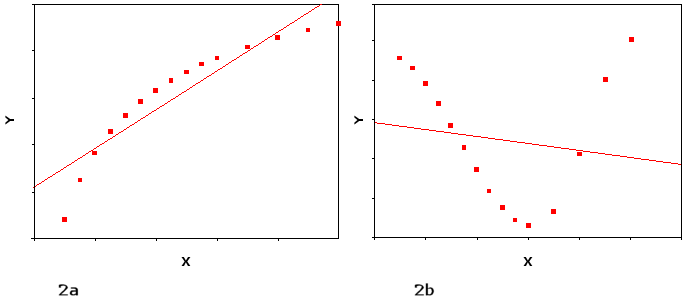
Kuvion 4 kummassakin esimerkissä pisteet tarkoittavat muuttujien havaittuja arvoja ja suora on niiden pohjalta piirretty regressiosuora. Kuvion 4a tilanteessa x- ja y-muuttujien yhteys on epälineaarinen, mutta poikkeama lineaarisuudesta ei ole suuri. Tässä tilanteessa muuttujan x regressiokerroin olisi positiivinen ja se luultavasti antaisi kohtuullisen hyvän likiarvon muuttujien välisestä suhteesta.
Esimerkkikuviossa 4b lineaarinen yhteys kuvaa x- ja y-muuttujien välistä yhteyttä erittäin huonosti. Regressiosuora on lähes vaakasuora (eli regressiokerroin on lähellä nollaa), eli lineaarisesti tarkasteltuna muuttujien välillä ei ole yhteyttä. Muuttujilla on kuitenkin selkeä epälineaarinen yhteys toisiinsa. Kuviosta 4b myös huomataan, ettei residuaalien keskiarvo ole nolla selittävän muuttujien eri arvoilla. Jos residuaalien kesiarvo olisi nolla, kuvion punaiset pisteet osuisivat keskimäärin regressiosuoralle eri x-muuttujan arvoilla.
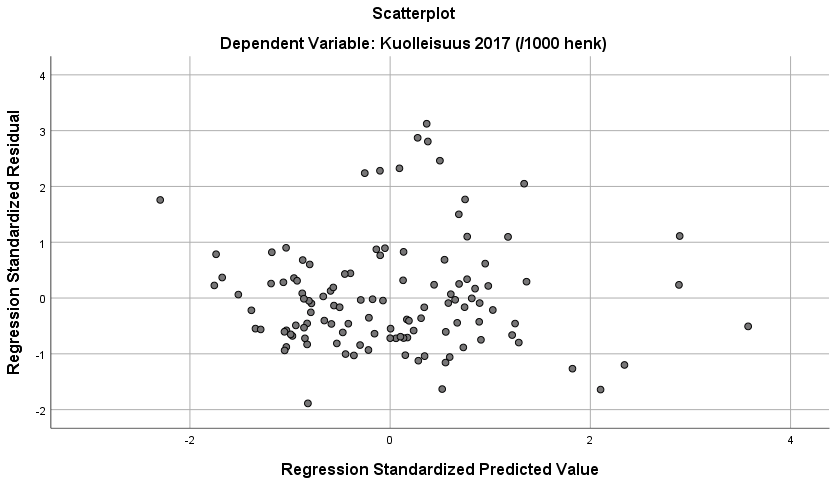
Yhteyden lineaarisuutta voidaan siis tarkastella empiirisesti residuaalien jakauman kautta. Tarkastelussa voidaan käyttää regressiomallin ennustamien arvojen ja standardoitujen residuaalien välistä yhteyttä havainnollistavaa sirontakuviota (Kuvio 5). (Kuvion toteuttaminen käsitellään SPSS-harjoituksessa 2). Kuviossa mallin standardoidut residuaalit tulevat y-akselille ja ennustetut arvot x-akselille. Otetaan esimerkiksi usean muuttujan regressiossa käytetty regressiomalli. Mallin estimoinnin jälkeen aineiston havainnoille lasketaan standardoidut residuaalit (poikkeamat ennustetuista arvoista). Sitten standardoidut residuaalit sijoitetaan kuvioon yhdessä mallien ennustamien arvojen kanssa. Esimerkin tapauksessa selkeää epälineaarista yhteyttä ei ilmene (kuten vaikkapa kuviossa 4b), joskaan residuaalien jakauma (y-akseli) ei näytä tasaiselta eri ennustearvoilla (x-akseli). Mikäli selittävien muuttujien ja selitettävän muuttujan välinen yhteys olisi epälineaarinen, kuvioon tulisi olla sovitettavissa jonkinlainen epälineaarinen käyrä (kuten esimerkkikuvioissa 4a tai 4b).
Regressioanalyysin avulla voidaan tarkastella myös muuttujien epälineaarisia suhteita. Tämä tapahtuu esimerkiksi muuttujamuunnosten avulla. Muunnoksen kohteena voi olla sekä selitettävä tai selittävät muuttujat tilanteen mukaan. Lievien epälineaarisuuksien korjaamiseen käytetään usein logaritmi- tai neliöjuurimuunnosta. Jos kuvion esimerkissä 4a x-muuttujasta otetaan luonnollinen logaritmi ja tämä uusi muuttuja sisällytetään regressioanalyysiin alkuperäisen x-muuttujan sijasta, paranee mallin selitysosuus huomattavasti. Tämä johtuu siitä, että y-muuttujalla ja uudella selittävällä muuttujalla (x:n logaritmi) on lähes täydellinen lineaarinen riippuvuus toisistaan.
Esimerkissä 4b epälineaarisuus on niin vahva, että yksinkertainen muuttujamuunnos tuskin korjaa ongelmaa. Muuttujien välinen yhteys on kuitenkin sellainen, että se voidaan kuvata toisen asteen yhtälöllä. Käytännössä tämä tarkoittaa sitä, että regressioanalyysia varten luodaan uusi muuttuja, joka saa arvoksi X-muuttujan arvon neliön (eli X^2). Kun uusi muuttuja lisätään regressioanalyysiin alkuperäisen selittävän muuttujan lisäksi, voidaan esimerkin mukainen epälineaarinen yhteys analysoida regressioanalyysin avulla.
Malliin voidaan lisätä alkuperäisen muuttujan ja sen neliön lisäksi myös kolmanteen potenssiin korotettu termi, jolloin voidaan mallintaa vielä monimutkaisempia epälineaarisia yhteyksiä. Tällaisten pollynomitermien lisääminen malliin on joustava tapa mallintaa hyvin erilaisia epälineaarisia yhteyksiä. Toisaalta epälineaarisia yhteyksiä voidaan mallintaa myös muilla kuin lineaarisilla regressiomalleilla (esimerkiksi logistinen regressiomalli tai poisson-regressio).
Residuaalien heteroskedastisuus ja normaalijakautuneisuus

Kuvion 5 sirontakuviossa tarkastellun regressiomallin residuaalien jakauma näytti jossain määrin epätasaiselta. Kuvion perusteella residuaalien hajonta näyttäisi esimerkiksi olevan isointa nollaa lähellä olevien ennustettujen arvojen kohdalla. Tämä viittaa siihen, ettei lineaarisen regression homoskedastisuusoletus luultavasti täyty. Toisin sanoen residuaalien jakauma olisi heteroskedastinen.
Heteroskedastisuus viittaa tilanteeseen, jossa regressiomallin virhetermien hajonta vaihtelee selvästi ja systemaattisesti x-muuttujien arvojen muuttuessa. Kuviossa 6 havainnollistetaan heteroskedastisuutta. Kuvion y-akseli kuvaa selitettävän muuttujan arvoja ja x-akseli selittävän muuttujan arvoja. Kuvion esittämässä tilanteessa on kyse heteroskedastisuudesta siksi, että virhetermit vaihtelevat regressiosuoran ympärillä huomattavasti enemmän silloin kun x-muuttuja saa suuria arvoja. Heteroskedastisuudella ei oikeastaan ole haitallista vaikutusta regressiokertoimien arvoon, mutta se häiritsee tilastollista päättelyä.
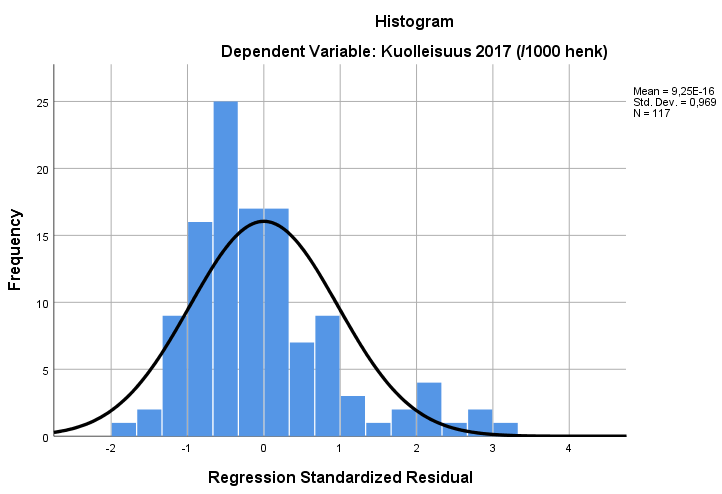
Toinen lineaarisen regressioanalyysin residuaalien jakaumaa koskeva oletus on residuaalien normaalijakautuneisuus. Tätä oletusta voidaan tarkastella kuten minkä tahansa muuttujan jakaumaa piirtämällä histogrammikuvio standardoituista residuaaleista. Kuviossa 7 on esitetty histogrammin avulla regressiomallin standardoitujen residuaalien jakauma. Kuvion perusteella residuaalit eivät näytä noudattavan normaalijakaumaa.
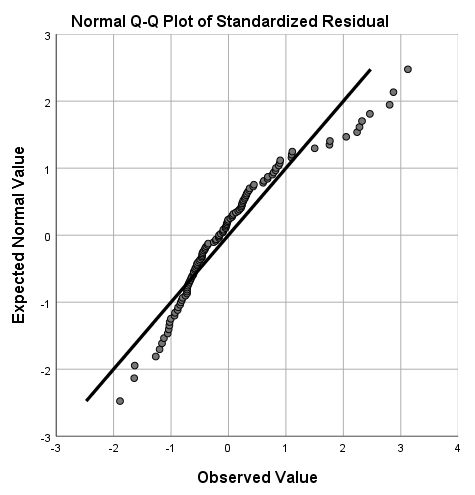
Residuaalien normaalijakautuneisuutta voidaan kuitenkin analysoida vielä tarkemmin kvantiilikuvion (QQ-plot) avulla (kuvio 8). Se vertaa havaittuja residuaalien jakaumaa teoreettiseen normaalijakaumaan. Mikäli residuaalit noudattavat normaalijakaumaa, pisteiden tulisi ryhmittyä kuvion poikki kulkevalle viivalle. Kuviosta huomataan, että residuaalien jakauma poikkeaa normaalijakaumasta etenkin "häntien kohdalla" eli jakauman ylä- ja alakvantiileissa. Näyttää siis siltä, että regressioanalyysin oletukset eivät esimerkkimallin tapauksessa täyty. Esimerkkitapauksessa voisi siis olla viisasta esimerkiksi käyttää väljempiin residuaalien jakaumaa koskeviin oletuksiin perustuvia keskivirheiden estimointimenetelmiä.
Ongelmien huomioiminen analyysissa

Regressiomallin arvioinnissa havaitut ongelmat kuten poikkeavat havainnot tai poikkeamat lineaarisen regressioanalyysin oletuksista on mahdollista huomioida analyyseissa. Siinä tapauksessa niiden vaikutus regressiokertoimiin ja tilastolliseen päättelyyn minimoidaan. Ongelmia kohdatessaan tutkijan kannattaa ensimmäisenä miettiä, onko mallissa jokin olennainen puute. Puuttuuko mallista esimerkiksi olennaisia muuttujia? Ongelmien ratkaisemiseen on useita muita tapoja, joista tässä yhteydessä käsitellään väljempiin oletuksiin perustuvia keskivirheiden estimointimenetelmiä, muuttujamuunnoksia ja yleistettyjä regressiomalleja (Darlington & Hayes, 2017).
Jos regressiomallin tarkastelussa esiintyy poikkeavia havaintoja tai poikkeamia virhetermin jakaumaan liittyvissä regressio-oletuksista, voidaan analyyseissa käyttää väljempiin oletuksiin perustuvia keskivirheiden estimointimenetelmiä. Näitä menetelmiä käytettäessä poikkeamat eivät vääristä tilastollista päättelyä. Ne eivät kuitenkaan välttämättä korjaa esimerkiksi poikkeavista havainnoista johtuvia vaikutuksia regressionkertoimiin. Poikkeamille vähemmän herkkiä keskivirheiden estimointimenetelmiä ovat esimerkiksi Huber–White -estimointi ja bootsrapping-estimointi.
Huber-White -keskivirheet eivät ole yhtä herkkiä virhetermin jakaumasta johtuville poikkeamille tai poikkeaville havainnoille. Tämän estimointimenetelmän käyttö siis parantaa tilastollisen päättelyn luotettavuutta, mikäli mallissa havaitaan niihin liittyviä ongelmia. Toisaalta näitä estimaattoreita voi yleensä käyttää melko luotettavasti, vaikka esimerkiksi homoskedastisuusoletuksesta poikkeaminen olisi vähäistä. Nämä estimaattorit ovat nykyään laajasti edustettuna eri tilasto-ohjelmistoissa (esimerkiksi SPSS-macro RLM).
Bootstrapping ei perustu oletuksiin residuaalien jakaumasta, vaan jakauma päätellään aineistosta. Menetelmässä arvotaan takaisinpalautuksen avulla suuri määrä "uusia otoksia" olemassa olevasta aineistosta. Analyysi toistetaan näillä eri otoksilla ja parametrien jakaumat lasketaan niiden perusteella. Bootstrap perustuu useisiin toistoihin. Jos esimerkiksi toistamme tietyn regressiomallin 10 000 kertaa uudelleen arvotulla otoksella, saamme yhtä monta arvoa jokaiselle regressiokertoimelle. Näiden 10 000 eri estimaatin avulla voidaan muodostaa esimerkiksi regressiokertoimen 95 %:n luottamusväli laskemalla, mille välille 95 prosenttia havaituista kertoimista sijoittui. Moni tilastollinen ohjelmisto tukee nykyään bootstrapping-estimointia.
Ylläkuvattujen estimointimenetelmien kohdalla on syytä muistaa, että ne eivät kuitenkaan ole taikatemppuja, jotka saavat ongelmat katoamaan (ks. esimerkiksi havaintojen poistaminen yllä kohdassa Poikkeavat havainnot eli outlier-tapaukset). Jos mallin taustalla on esimerkiksi vakavia poikkeamia lineaarisuusoletuksesta, kannattaa mieluummin harkita vaikkapa muuttujamuunnoksia tai yleistettyjä regressiomalleja. Muuttujamuunnosten avulla vastemuuttujan tai selittävien muuttujien jakaumaa muutetaan siten, että se sopii paremmin lineaarisen regressiomallintamiseen. Mahdollisia muuttujamuunnoksia ovat esimerkiksi logaritminen tai neliöjuurimuunnos. Muuttujamuunnosten yksi ongelma on, että sen jälkeen muuttujat eivät enää ole luennollisella skaalalla, mikä vaikeuttaa tulkintaa.
On myös mahdollista, ettei lineaarinen yhtälö ole paras tapa estimoida tutkittavien muuttujien välistä yhteyttä. Siinä tapauksessa tutkija voi käyttää yleistettyjä lineaarisia malleja, jotka perustuvat epälineaaristen yhteyksien analysoimiseen. Tällaisia malleja ovat esimerkiksi logistinen regressioanalyysi tai poisson-regressio. Nämä mallit eivät oleta, että selitettävän muuttujan yhteys vastemuuttujaan olisi lineaarinen.