Monitasomallit
Noora Ellonen & Markus Kaakinen (viittausohje)
Tämä on kuudes ja viimeinen osa regressioanalyysista kertovassa luvusta ja pääset alla olevasta listasta siirtymään suoraan muihin luvun osiin.
Regressioanalyysi on yksi yleisimmistä monimuuttujamenetelmistä yhteiskunta- ja ihmistieteissä. Regressioanalyysin erityinen etu on se, että sillä voidaan tutkia useamman muuttujan yhtäaikaista yhteyttä selitettävään ilmiöön.
Kiinnostuksen kohteena on usein sosiaalisen ympäristön ja yksilön välinen suhde. Yksilötekijöiden ohella ollaan siis esimerkiksi kiinnostuneita siitä, miten työpaikan ilmapiiri vaikuttaa työssä viihtymiseen tai miten koulujen koko vaikuttaa oppilaiden oppimistuloksiin. Tutkimuskysymykset rakentuvat myös usein siitä näkökulmasta, että erilaisia ryhmiä verrataan toisiinsa. Monitasomallit kuten hierarkkinen lineaarinen regressioanalyysi ovat tavallisten regressioanalyysien laajennuksia, ja ne on tarkoitettu tällaisten tutkimuskysymysten ratkaisemiseen.
Monitasomallit soveltuvat sellaisten (hierarkkisten) aineistojen analysointiin, joissa havainnot eivät ole toisistaan riippumattomia (ks. Lineaarisen regressioanalyysin oletukset, oletus 7). Monitasomallien perusajatus on selittää yksilötason ilmiöitä sekä yksilötason että ryhmätason tekijöillä. Toisaalta monitasomalleilla voidaan analysoida myös pitkittäisaineistoja, joissa yhdestä yksilöstä on aineistossa useampi havaintokerta. Tällaisissa pitkittäisasetelmissa voidaan analysoida yksilöiden sisäistä muutosta ja sen yhteyttä persoonallisuuden kaltaisiin verrattain pysyviin ominaisuuksiin ja toisaalta ajassa vaihteleviin tekijöihin (kuten työttömyys tai rikosuhrikokemukset). Näin voidaan tarkastella samalla sekä pysyvämpiä yksilöiden välisiä eroja että yksilöiden sisäistä muutosta. Hierarkkisissa aineistossa voi olla mukana myös useampia tasoja.
Monitasomallin käsitteestä

Tutkimuskirjallisuudessa monitasoisista regressioanalyyseistä käytetään eri nimityksiä. Tilastotieteellisesti orientoituneet suosivat usein sekamalli-termiä (engl. mixed models). Yhteiskunta- ja ihmistieteissä näkee käytettävän yleistä monitasomalli-nimitystä (multilevel model), mutta kuten yksitasoisissa regressioanalyyseissä, monitasoisissakin regressioanalyyseissä erotetaan usein jo käsitteellisellä tasolla lineaariset mallit muista. Monitasoisesta lineaarisesta regressioanalyysistä käytetään muun muassa nimityksiä hierarkkinen lineaarinen malli (hierarchical linear model), satunnaiskertoimien malli (random coefficient model) ja varianssikomponenttimalli (variance component model). Lineaarisille vaste- eli selitettäville muuttujille soveltuvien mallien lisäksi monitasomalleja voidaan rakentaa muunkin tyyppisille vastemuuttujille (non-linear models ja generalized linear models). Tässä artikkelissa keskitytään kaksitasoiseen hierarkkiseen lineaariseen malliin.
Hierarkkinen aineisto

Hierarkkisella aineistolla tarkoitetaan aineistorakennetta, jossa havainnot muodostavat erilaisia ryhmiä ja jossa selittäviä tekijöitä on useammalla tasolla. Kuviossa 1 on kuvattu esimerkki kaksitasoisesta aineistosta. Kiinnostuksen kohteena olevat yksilöt muodostavat aineiston ensimmäisen tason. Yksittäiset havainnot ovat ryhmittyneet ryhmiin, jotka muodostavat aineiston toisen tason. Tyypillinen esimerkki hierarkkisesta aineistosta on koululaisista muodostuva aineisto, jossa ensimmäisellä tasolla ovat oppilaat ja toisella tasolla luokat. Jos kouluja olisi useita, ne voisivat muodostaa kolmannen tason. Tasojen määrää ei periaatteessa ole rajoitettu. Toisaalta kuvio 1 voisi viitata asetelmaan, jossa tasolla yksi ovat samasta yksilöstä eri aikana saadut havainnot. Siinä tapauksessa yksilöt muodostaisivat tason kaksi. Yksilöt voisivat toki edelleen sijoittua esimerkiksi luokkiin tasolle kolme. Tässä artikkelissa keskitytään kuitenkin kaksitasoiseen analyysiin, jossa yksilöt (taso 1) sijoittuvat ryhmiin (taso 2). Monitasomallien käytöstä pitkittäisanalyyseissa löytyy hyviä johdatuksia muualta (esim. Bliese & Ployhart, 2002).
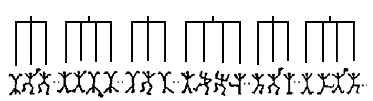
Hierarkkinen lineaarinen regressio

Hierarkkiset lineaariset mallit ovat tavallisen lineaarisen regression laajennuksia. Yksitasoisessa regressioanalyysissä selitetään vastemuuttujaa saman tason selittäjillä. Tavoitteena on selittää mahdollisimman suuri osa vastemuuttujan varianssista. Hierarkkisissa lineaarisissa regressiomalleissa on sama tavoite. Siinä selitettävä muuttuja on ykköstasolla mutta selittäjiä on vähintään kahdella tasolla. Yksilötason tekijöillä selitetään vastemuuttujan vaihtelua ryhmien sisällä ja ryhmätason tekijöillä selitetään ryhmien välisiä eroja vastemuuttujan vaihtelussa. Toisin sanoen yksitasoisessa regressioanalyysissä selitetään ilmiön vaihtelua yksilöiden välillä, kun taas sekamallissa selitetään ilmiön vaihtelua sekä yksilöiden että ryhmien välillä.
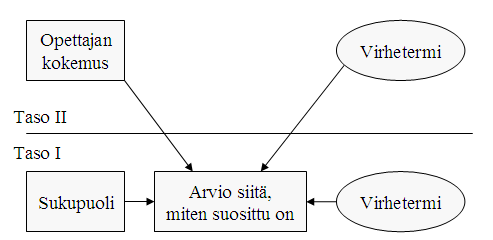
Kuviossa 2 on kuvattu artikkelin ja sen harjoituksen esimerkki kaksitasoisena tutkimusasetelmana. Selitettävä muuttuja kuvaa, kuinka suosituksi oppilaat kokevat itsensä koulussa. Tätä selitetään yksilötason muuttujalla, joka on oppilaan sukupuoli, sekä ryhmätason muuttujalla, joka on opettajan työkokemuksen pituus. Ajatuksena on, että opettajan työkokemuksen pituus lisää opettajan taitoja suhtautua oppilaisiin tasapuolisesti ja vaikuttaa oppilaiden suhtautumiseen toisiinsa, ja siten opettajan työkokemuksen pituudella voisi olla yhteys siihen, miten suosituksi oppilas kokee itsensä.
Koska analyysi on kaksitasoinen, on mallissa myös kaksi virhetermiä eli residuaalia. Alemman tason virhetermi kuvaa sitä, paljonko suosion vaihtelusta jää selittymättä yksilötasolla ja ylemmän tason virhetermi sitä, paljonko suosion vaihtelusta jää selittymättä koulutasolla.
Toisen tason mukaan ottaminen tuo regressiomalliin uusia parametreja. Yksitasoinen lineaarinen regressio merkitään tyypillisesti:
jossa b0\( b_0 \) on vakiotermi (intercept), b1\( b_1 \) on regressiokerroin (regression slope) ja ei\( e_i \) on virhetermi (residual error term). Vakiotermi viittaa selitettävän muuttujan arvoon silloin, kuin selittävä muuttuja saa arvon nolla, eli regressiosuora leikkaa y-akselin. Regressiokerroin on regressiosuoran kulmakerroin. Virhetermi kuvaa sitä, kuinka kaukana havainnot ovat keskimäärin regressiosuorasta, eli kuinka paljon selitettävän muuttujan vaihtelusta jää selittymättä.
Kun yksitasoisesta regressioanalyysistä tehdään kaksitasoinen, lisätään kaavaan ryhmittelevän muuttujan vaikutus. Huomioidaan siis se, että vastemuuttujan vaihtelu voi olla erilaista eri ryhmissä. Seuraavassa kaavassa on edelleen pelkästään ensimmäisen tason selittäjiä, mutta aineiston hierarkkinen rakenne on huomioitu lisäämällä siihen ryhmää ilmaiseva indeksi j:
jossa b0j \( b_{0j} \) on vakio (intercept), b1j\( b_{1j} \) on regressiokerroin (regression slope) ja eij\( e_{ij} \) on virhetermi (residual error term).
Hierarkkisessa mallissa kukin ryhmä voi saada oman vakiotermin, regressiokertoimen ja virhetermin. Jotta yksilötaso ja ryhmätaso erottautuisivat malleissa, käytetään hierarkkisten mallien kaavamerkinnässä alanotaatioita i \(_i\) ja j \(_j\) . Alanotaatio i \(_i\) viittaa yksilötasoon ja j \(_j\) ryhmätasoon. Yksilötason virhetermiä kuvataan yksitasoiselle regressioanalyysille tyypillisillä e-termeillä. Hierarkkisessa mallissa siihen kuitenkin lisätään monitasoisuutta kuvaavat alanotaatiot, jolloin yksilötason virhetermiä merkitään termillä eij \(e_{ij}\). Toisen tason virhetermeihin viitataan u-termeillä: u0j, u1j, u2j jne. \(u_{0j},u_{1j},u_{2j}\) jne.
Miksi ryhmätason vaikutus tulee huomioida?

Edellä kuvattu esimerkki on varsin tyypillinen regressioanalyysiin soveltuva tutkimuskysymys: miten oppilaan sukupuoli ja opettajan työkokemus vaikuttavat siihen, miten suosituksi oppilas kokee itsensä koulussa. Miksi siihen ei voida käyttää tavallista yksitasoista lineaarista regressioanalyysiä?
Ensisijainen ongelma on se, että yksitasoisen regressioanalyysin käyttö hierarkkisessa aineistossa ei täytä tavanomaisen lineaarisen regressioanalyysin oletuksia. Lineaarisen regressioanalyysin perusolettamus on, että havainnot ovat toisistaan riippumattomia. Hierarkkisessa aineistossa tämä olettamus ei täyty. Havainnot eivät ole riippumattomia toisistaan, sillä samaan ryhmään kuuluvat muistuttavat oletettavasti enemmän toisiaan kuin kaksi eri ryhmän jäsentä. Havainnot ovat ikään kuin altistuneet ryhmän samanlaistavalle vaikutukselle kiinnostuksen kohteena olevassa ilmiössä. Tämän seurauksena analyysin virhetermit eivät ole riippumattomia toisistaan.
Toinen rajoite tavallisessa lineaarisessa regressioanalyysissä on se, että siinä ei voi käyttää selittäjiä useammalta eri tasolta. Tämä ongelma on perinteisesti ratkaistu disaggregoinnin tai aggregoinnin avulla. Disaggregoinnissa eritasoisia muuttujia muokataan siten, että niitä kaikkia voidaan tarkastella alimmalla tasolla. Aggregoinnissa sitä vastoin kaikki muuttujat muokataan soveltuviksi ylimmälle tasolle. Tämä ei kuitenkaan ratkaise riippumattomuusolettamuksen rikkomista, jolloin disaggregoidut tai aggregoidut muuttujat eivät toimi luotettavina selittäjinä. Hierarkkinen lineaarinen regressioanalyysi, kuten monitasomallit yleensäkin, ottavat huomioon aineiston klusteroitumisen, eli havaintojen riippuvuuden ryhmittäin, ja mahdollistavat myös eritasoisten selittäjien käytön.
Ryhmätason muuttuja

Jotta yksilötason ilmiötä voidaan selittää ryhmätason tekijällä, ryhmätason tekijällä tulee olla todellinen ryhmittelevä vaikutus. Analyysitasolla ryhmään kuulumisen kriteerin tulee siis olla selkeä. Kaikilla samaan ryhmään kuuluvilla tulee olla ryhmittelevässä muuttujassa sama arvo, kaikkien havaintojen tulee kuulua johonkin ryhmään, ja ryhmien tulee olla toistensa poissulkevia. Aineiston hierarkkisuus empiirisellä tasolla tuleekin aina tarkistaa ennen mallin rakentamista.
Jotta tulokset ovat mielekkäitä, ryhmittelevän muuttujan tulee olla myös teoreettisella tasolla selkeä ja todellinen. Monissa yhteiskunta- ja ihmistieteen tutkimusasetelmissa ryhmien väliset rajat ja ryhmään kuuluminen eivät ole aina täysin yksiselitteisiä. Ryhmätason muuttujien operationalisointi tuleekin tehdä huolella ja näennäisiä ryhmittelyjä tulee välttää. Joop Hoxin teos (2010, 7) kuvaa tarkemmin monitasoisten asetelmien hahmottamista teoreettisella tasolla.
Varianssin jakaminen

Hierarkkisessa lineaarisessa mallissa on siis selittäjiä ja virhetermejä kahdella tasolla. Lähtöoletuksena on, että selitettävän ilmiön vaihtelu selittyy sekä ryhmien välillä (taso 2) että ryhmien sisällä (taso 1). Esimerkiksi oppilaiden keskimääräinen arvio siitä, kuinka suosittu hän on, voi vaihdella erilaisten ja eri alueilla sijaitsevien koulujen välillä (tasolla 2). Toisaalta oppilaat eroavat myös koulujen sisällä sen suhteen, kuinka suosittuina he itseään pitävät (taso 1). Varianssin jakamisen myötä mallissa on myös varianssitermejä kahdella tasolla. Virhetermeistä estimoidut eri tasojen varianssit ovat toisistaan riippumattomia. Analyysissä tarkastellaan, miten mukaan tuodut selittäjät selittävät toisaalta yksilötason varianssia ja toisaalta ryhmätason varianssia.
Varianssin kautta saadaan selville myös se, missä määrin kiinnostuksen kohteena oleva ilmiö on ylipäätään selitettävissä yksilötason tai ryhmätason ilmiöillä. Toisin sanoen varianssin jakamisen avulla voidaan tarkistaa aineiston hierarkkinen rakenne: onko ryhmätason tekijöillä merkitystä kiinnostuksen kohteena olevaan ilmiöön. Jos varianssia ei olisi lainkaan tasolla 2, kaikki koulut olisivat esimerkiksi samanlaisia oppilaiden itse havaitseman suosion suhteen. Jos taas tasolla 1 ei olisi lainkaan varianssia, koulun kaikki oppilaat kokisivat olevansa täysin yhtä suosittuja.
Ryhmätason vaikutuksen suuruus voidaan laskea niin sanotun sisäkorrelaation (intraclass correlation) avulla. Sisäkorrelaatiota merkitään usein rholla (ρ). Sisäkorrelaatio kuvaa, kuinka paljon varianssista on selitettävissä ylemmän tason tekijöillä. Sisäkorrelaatio lasketaan jakamalla ryhmätason varianssi ryhmätason (σ2u0) ja yksilötason (σ2e) varianssien summalla. Tulos kertoo prosentteina sen, missä määrin vastemuuttuja on selitettävissä ryhmätason ilmiöllä.
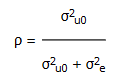
Kiinteitä ja satunnaisia osia

Hierarkkisissa lineaarisissa malleissa voidaan tarkastella sekä kiinteitä (fixed) että satunnaisia (random) vaikutuksia. Samoilla selittävillä muuttujilla voidaan siten rakentaa useita erilaisia malleja. Etukäteen on hankala usein tietää, mikä malleista on toimivin. Monitasoanalyysejä onkin hyvä rakentaa vaiheittain ja verrata erilaisia malleja keskenään (esim. Bliese & Ployhart, 2002).
Satunnaisuudella tarkoitetaan sitä, että annetaan satunnaisena pidettävän estimaatin vaihdella ryhmien välillä. Kiinteällä vaikutuksella tarkoitetaan sitä, että yhteys on samanlainen kaikissa ryhmissä. Erilaisia malleja nimetään usein sen mukaan, missä määrin mallissa on satunnaisia tekijöitä.
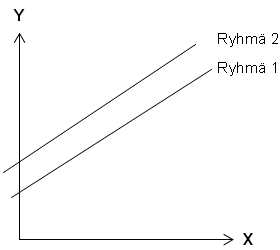
Satunnaisen vakion (random intercept) malleissa vakiotermin annetaan vaihdella ryhmien välillä, mutta pidetään regressiokerroin kiinteänä (kuvio 3). Jokainen ryhmä saa siten oman regressiosuoransa. Regressiosuorat ovat samansuuntaisia ja niiden kulmakerroin on yhtä suuri, mutta niiden lähtötaso vaihtelee. Toisin sanoen ne laikkaavat Y-akselin eri kohdissa. Tällöin satunnaisosa ja virhetermi u0j\( u_{0j} \) liittyvät vakioon, eli
jossa γ00 \(y_{00}\) on itse vakio, eli periaatteessa ryhmien yleinen keskiarvo ja u0j> \(u_{0j}\) on sen virhetermi, joka kuvaa ryhmien välistä vaihtelua vakiossa.
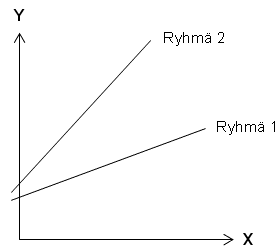
Satunnaisten regressiokertoimien (random slope) mallista puhutaan puolestaan silloin, kun regressiokerrointen annetaan vaihdella ryhmien välillä. Jokaiselle ryhmälle siis lasketaan oma regressiokerroin, jolloin regressiosuorien kulmakertoimet ovat erilaisia ryhmien välillä (kuvio 4). Tällöin satunnaisosa ja virhetermi liittyvät regressiokertoimeen:
jossa γ10 \(\gamma_{10} \) on vakio ja u1j \(u_{1j} \) sen residuaali. Mallia, jossa sekä vakion että regressiokertoimen annetaan vaihdella satunnaisesti, kutsutaan random coefficient -malliksi eli satunnaiskertoimien malliksi.
Edellisissä esimerkeissä oli mukana vain ensimmäisen tason selittäjiä. Mikäli mallissa on lisäksi toisen tason selittäjiä (Z), lisätään ne malliin seuraavasti:
jossa γ00 + γ01\(\gamma_{00} \) + \(\gamma_{01} \) ovat vakio ja regressiokerroin, jotka määrittävät vakion b0j \(b_{0j}\) tilanteessa, jossa ryhmätason muuttuja Z\(Z\) on huomioitu. Malliin voidaan myös lisätä sellaisia tason 2 muuttujia, jotka selittävät regressiokeroimen vaihtelua ryhmien välillä:
jossa γ10 + γ11\(\gamma_{10} \) ja \( \gamma_{11}\) ovat vakio ja regressiokerroin, jotka määrittävät selittävän muuttujan b1j\(b_{1j}\) vaikutuksen tilanteessa, jossa muuttuja Z\(Z\) on huomioitu.
Ryhmätason selittäjät siis selittävät joko vakion tai regressiokerrointen vaihtelua ryhmien välillä. Se, että ryhmätason muuttuja ennustaa vakiota, viittaa suoriin vaikutuksiin. Se, että ryhmätason muuttuja ennustaa regressiokertoimia, viittaa interaktiovaikutukseen tasojen välillä (cross-level interaction).
Kun otetaan huomioon selittäjät kahdelta eri tasolta, saadaan monitasomallin lausekkeeksi:
Yhtälössä on periaatteessa kaksi osaa:
joka sisältää kaikki kiinteät kertoimet (fixed coefficients). Tätä osaa kutsutaankin usein mallin kiinteäksi osaksi.
sisältää puolestaan kaikki satunnaiset virhetermit (random errors) ja tätä osaa kutsutaan mallin satunnaisosaksi. Ne siis kuvaavat sitä, missä määrin tason yksi ennustetut arvot poikkeavat havaituista arvoista ja toisaalta, missä määrin vakiotermissä ja regressiokertoimessa on vaihtelua ryhmien välillä.
Mitä enemmän mallissa on satunnaisparametreja, sitä enemmän malliin tulee myös varianssitermejä. Kuten sisäkorrelaation yhteydessä jo tuotiin esiin, ensimmäisen tason virhetermin (eij \( e_{ij} \) ) varianssia merkitään termillä σe2 \( \sigma^2_{e} \) ja toisen tason virhetermin (u0j \( u_{0j} \) ) varianssia merkitään termillä σ2u0 \( \sigma^2_{u0} \) . Satunnaisparametrien myötä mukaan tulee toisen tason u1j \( u_{1j} \) virhetermin varianssi, jota merkitään termillä σ2u1 \( \sigma^2_{u1} \) . Tämä varianssitermi viittaa ryhmien välisten regressiokerrointen vaihteluun. Tuomalla ryhmätason muuttujia malliin halutaan usein pienentää tätä varianssia, eli löytää syitä sille, miksi selittäjän ja vastemuuttujan välinen yhteys vaihtelee ryhmien välillä. Lisäksi mallissa on termien u0j \( u_{0j}\) ja u1j \( u_{1j} \) kovarianssi, jota merkitään termillä σu01 \( \sigma_{u01} \) . Tässä artikkelissa ei perehdytä kovarianssin tulkintaan, mutta se on silti keskeinen osa monitasomallinnusta.
Sekamallien tai satunnaisketoimien mallien ohella tutkijalla on myös muita mallinnusvaihtoehtoja. Yksi näistä on kiinteiden vaikutusten malli (fixed effects model). Näissä malleissa ensimmäisten (yksilö)tason yhteydet pakotetaan samoiksi eri kakkostason (esim. koululuokat) välillä. Niiden ei siis anneta vaihdella yksilöiden välillä. Mallin tulokset kertovat yhteyksistä tasolla 1, kun mahdolliset erot tasolla 2 on otettu huomioon.
Mallin rakentaminen vaiheittain

Mitä enemmän mallissa on satunnaisparametreja, sitä monimutkaisemmaksi malli muodostuu. Useiden satunnaisparametrien malli voi olla hankalasti tulkittavissa. Useat satunnaisparametrit voivat joskus olla myös haaste tarkasteltaessa mallin hyvyyttä. Mallin toimivuuden ja tulkittavuuden näkökulmasta onkin kannattavaa tarkastella mallissa satunnaisvaikutuksena vain niitä muuttujia, joiden satunnaisvaikutus on merkityksellinen verrattuna vaikutuksen tarkasteluun kiinteänä. Tämän selvittämiseksi malli on syytä rakentaa vaiheittain ja verrata malleja keskenään.
Toinen syy mallin vaiheittaiselle rakentamiselle on se, että muuttujien vaikutuksia tarkastellaan usein paitsi muuttujan estimaatin avulla myös siltä kannalta, miten eri tasojen varianssit muuttuvat muuttujan tullessa malliin. Myös tämä edellyttää usein mallin vaiheittaista rakentamista.
Hierarkkisen (2-tasoisen) lineaarisen regressiomallin tyypilliset vaiheet:
- Nollamalli (intercept-only model)
- Nollamallissa malliin otetaan mukaan vain vakiotermi ja virhetermit sekä yksilö- että ryhmätasolle. Nollamallissa ei siis ole mukana selittäjiä. Nollamallilla saadaan selville, miten varianssi jakautuu yksilö- ja ryhmätasolle. Sen perusteella voidaan laskea sisäkorrelaatio.
- Lisätään ensimmäisen tason selittäjä(t)
- Ensimmäisen tason selittäjät kannattaa yleensä lisätä malliin ensin niin sanottuina kiinteinä vaikutuksina (random intercept model). Tämän mallin kautta tarkastellaan muuttujien estimaatteja ja sitä, miten varianssi yksilö- ja ryhmätasolla muuttuu.
- Lisätään ryhmätason selittäjä(t)
- Lisätään malliin ryhmätason selittäjä ja tarkastellaan, paljonko sekä yksilö- että ryhmätason varianssi selittyy sillä, että otetaan toisen tason muuttujat mukaan.
- Satunnaiskertoimien malli
- Tarkastellaan yksilötason muuttujien vaikutusta satunnaisena ja verrataan, tuoko se lisäarvoa suhteessa siihen, että muuttujan vaikutusta tarkasteltaisiin kiinteänä (random slope model). Tarkastelu on hyvä tehdä erikseen kunkin selittäjän osalta.
- Cross level -interaktiomalli
- Mikäli mallissa on mukana yksilötason selittäjiä (regressiokertoimia) satunnaisvaikutuksena, voidaan vielä tarkastella tasojen välistä interaktiota. Tällöin tarkastellaan, selittääkö joku ryhmätason muuttuja ryhmien välisiä eroja regressiokertoimissa.
Mallin arviointi

Regressioanalyyseille tyypilliseen tapaan hierarkkisessa lineaarisessa mallissa pyritään selittämään mahdollisimman kattavasti vastemuuttujan varianssia. Voidaankin ajatella, että mitä enemmän malli selittää vastemuuttujan varianssista eri tasoilla, sitä parempi malli on kyseessä. Muuttujille voidaan laskea R2-selitysosuus varianssista. Sen lisäksi on kuitenkin syytä tarkastella yleisemmin sitä, miten hyvin malli istuu aineistoon, eli miten hyvin mallissa havaitut arvot vastaavat odotusarvoja.
Koska hierarkkiset mallit rakennetaan vaiheittain, tarkoittaa mallin hyvyyden arviointi käytännössä eri vaiheiden vertailua. Mallien vertailu on oma tilastollisen testauksen maailmansa, johon ei tässä paneuduta, mutta mainittakoon muutama yleisesti käytetty SPSS:n automaattisesti tulostama tunnusluku.
Yksi tapa on tarkastella -2 Log Likelihood -arvon muutosta. Mitä pienempi arvo on, sitä paremmin malli istuu aineistoon. Vaihtoehtoisesti voi käyttää AIC-informaatiokriteereitä (Akaike’s) tai BIC-informaatiokriteereitä (Schwartz’s Bayesian). Myös niiden kohdalla malli on sitä parempi, mitä pienempi arvo on. On varsin yleistä, että mallien vertailussa raportoidaan yksinomaan testisuureen arvo arvioimatta sen enempää muutoksen tilastollista merkitsevyyttä. Merkitsevyys on tarvittaessa kuitenkin laskettavissa. Esim. -2LL -testisuureen muutos noudattaa khi2-jakaumaa ja vapausasteiden määrä määräytyy lisättyjen parametrien määrästä (lue lisää Snijders & Bosker 1999).
Monitasomallinnuksen luotettavuus riippuu myös aineiston koosta. Monitasomalleissa aineiston koko perustuu sekä kakkostason ryhmien määrään että ryhmien kokoon (eli havaintojen määrään ykköstasolla). Aineiston koon kannalta keskeisintä on, että ryhmiä on analyysissa mukana tarpeeksi. Ryhmien määrälle ei ole olemassa tarkka alarajaa, ja tarvittava määrä riippuu tutkittavasta ilmiöstä (ks. esim. Snijders & Bosker, 1993). Usein ajatellaan, että ryhmiä olisi hyvä olla vähintään 25, mutta myös tätä suuremmalla otoksella (esim. 50 ryhmää tai alle) ryhmien välisistä variansseista ja niiden tilastollisesta merkitsevyydestä voi olla haastavaa tehdä luotettavia päätelmiä (Maas & Hox, 2005; Snijders & Bosker, 1993). Myös silloin, kun ryhmien määrä on pieni, mallien regressiokertoimet ja niiden keskivirheet ovat kuitenkin luotettavia (Maas & Hox, 2005). Ryhmien pieni määrä ei siis ole samalla tavalla ongelma silloin, kun tutkimuksen tarkoitus on tarkastella regressiokertoimia ja niiden keskivirheitä (p-arvot).
Tulosten raportointi ja tulkinta

Vaiheittain rakennetut hierarkkiset mallit on hyvä myös raportoida vaiheittain. Eri vaiheet voidaan raportoida esimerkiksi samassa taulukossa. Taulukossa 1 on raportoitu tässä luvussa aiemmin käsitelty esimerkki hierarkkisesta lineaarisesta regressiomallista, joka selittää alakoulun oppilaiden käsitystä omasta suosittuudestaan (ks. myös SPSS-harjoitus 4). Mallissa tason yksi muodostavat oppilaat (yksilöt). Tason kaksi taas muodostavat luokat. Mallissa selitettävä muuttuja on oppilaiden kokemus siitä, kuinka suosittuja he ovat toisten oppilaiden keskuudessa. Selittävänä muuttujana tasolla 1 on oppilaan sukupuoli (0 = poika, 1 = tyttö). Tason kaksi selittäjä on luokan opettajan työkokemus vuosissa laskettuna. Malli on rakennettu viidessä osassa (ks. yllä Mallin rakentaminen vaiheittain).
| Nollamalli | Kiinteiden vaikutusten malli (yksilötason muuttuja) | Kiinteiden vaikutusten malli (luokkatason muuttuja) | Satunnaiskertoimien malli | Satunnaiskertoimien malli + interaktio | |
| Kiinteä osa | |||||
| Vakio | 5.31 | 4.90 (.10) | 3.56 (.17) | 3.34 (.16) | 3.31 (.16) |
| Sukupuoli | 0.84 (.03) | 0.84 (.03) | 0.84 (.06) | 1.33 (.13) | |
| Opettajan kokemus | 0.09 (.01) | 0.11 (.01) | 0.11 (.01) | ||
| Sp*OpeKokemus | -0.03 (.01) | ||||
| Satunnainen osa | |||||
| σe2 \( \sigma^2_{e} \) | 0.64 (.02) | 0.46 (.01) | 0.46 (.01) | 0.39 (.01) | 0.39 (.01) |
| σ2u0 \( \sigma^2_{u0} \) | 0.88 (.13) | 0.86 (.13) | 0.49 (.07) | 0.41 (.06) | 0.41 (.06) |
| σ2u1 \( \sigma^2_{u1} \) | 0.27 (.05) | 0.23 (.04) | |||
| σu01 \( \sigma_{u01} \) | 0.02 (.04) | 0.02 (.04) | |||
| -2LL \( -2LL \) | 5116 | 4493 | 4444 | 4276 | 4268 |
Taulukon perusteella näyttäisi siltä, että satunnaisten osien tuominen mukaan malliin parantaa mallia (-2LL-kerroin pienenee). Tosin satunnaisten elementtien aiheuttamaa muutoksen tilastollista merkitsevyyttä ei testata (katso esim. Bliese & Ployhart, 2002). Nollamallista voidaan laskea, että oppilaiden kokemus omasta suosittuudestaan muiden oppilaiden keskuudessa selittyy isolta osin luokkatasolla (ICC = 0,88/(0,88+0,64) = 0,58). Mallin perusteella tyttöjen käsitys omasta suosittuudestaan on poikia positiivisempi (B=0.84). Myös opettajan työkokemuksella vaikuttaa olevan merkitystä suosittuuden kokemuksen kannalta. Mitä enemmän luokan opettajalla on työvuosia, sen suositummiksi oppilaat arvioivat itsensä. Kerroin muuttuu hieman, kun mallin regressiokertoimien annetaan vaihdella luokittain (Satunnaiskertoimien malli). Opettajan kokemus selittää myös sukupuolen ja koetun suosittuuteen välisen yhteyden vaihtelua luokkien välillä. Interaktiovaikutus tasojen välillä (B = -0,03) on tilastollisesti merkitsevä. Mitä enemmän luokan opettajalla siis on työkokemusta, sitä pienempi on tyttöjen ja poikien välinen ero koetussa suosittuudessa.
Taulukosta 1 huomataan myös, että selittäjien lisääminen malliin vähentää selittämättömäksi jäävää vaihtelua. Ensimmäisen tason virhetermi (eij\( e_{ij} \)) pienenee, kun malliin lisätään selittäjiä. Samoin selittämätön osuus vakiotermin vaihtelusta ryhmien välillä (σ2u0\( \sigma^2_{u0} \)) laskee, kun malliin lisätään ryhmätason selittäjiä. Myös sukupuolen luokkakohtainen varianssi pienenee (σ2u1\( \sigma^2_{u1} \)), kun malliin lisätään sukupuolen ja opettajan kokemuksen välinen interaktio. Termien u0j ja u1j \( u_{0j} \) ja \( u_{1j} \) välinen kovarianssi (σu01\( \sigma_{u01} \)) ei sen sijaan ole merkitsevä. Toisin sanoen, sukupuolen yhteys koettuun suosittuuteen ei vaihtele sen mukaan, mikä on tietyn luokan koetun suosittuuden keskimääräinen taso.
Joskus tulosten tulkinnan haasteena on se, että hierarkkisessa lineaarisessa regressioanalyysissä raportoidut kertoimet ovat standardoimattomia kertoimia. Standardoimattomat kertoimet kuvaavat sitä, paljonko selitettävä muuttuja muuttuu selittävän muuttujan muuttuessa yhden yksikön. Jos muuttujien "yksiköille" on selkeä luonnollinen tulkinta, kuten esimerkiksi vuosi, tulkinta onnistuu myös standardoimattomien kertoimien avulla. Mutta jos mallissa on mukana muuttujia, joiden "yksikkö" ei sinällään ole helposti tulkittavissa, tulisi muuttujat standardoida, eli muuttujien mittausskaala huomioida, tulkinnan helpottamiseksi. Vastaava standardoinnin tarve liittyy myös tavallisiin regressioanalyyseihin, mutta niiden kohdalla tilasto-ohjelmat laskevat usein standardoidut kertoimet valmiiksi. Valitettavasti tilasto-ohjelmistot laskevat harvemmin standardoituja kertoimia hierarkkisten mallien osalta. Ne voi kuitenkin laskea käsin. Toisissa sovelluksissa voi vaihtoehtoisesti tehdä lisäanalyysejä niiden laskemiseksi.
Toinen tulosten tulkinnassa huomioitava asia on muuttujien keskittäminen (centering). Mielekkäimmän tulkinnan saamiseksi mallin lukuarvoille tulisi riippumattomat muuttujat keskittää. Keskittämällä muuttujille saadaan merkityksellinen nollakohta, jolloin niiden tulkinta ja vertailu keskenään on mielekkäämpää. Keskittäminen on tärkeää myös yksitasoisissa regressioanalyyseissä multikollineaarisuuden eli selittävien muuttujien suuren keskinäisen korreloinnin vähentämiseksi varsinkin, jos mallissa käytetään interaktiotermejä. Muuttujien keskittämisestä monitasoanalyyseissä voi lukea lisää Endersin ja Tofighin artikkelista (2007).
Tilasto-ohjelmat

SPSS-ohjelmalla on mahdollista tehdä hierarkkisia lineaarisia malleja. Sen sijaan epälineaarisissa malleissa SPSS on vielä varsin rajallinen. Muista yleisistä tilasto-ohjelmista muun muassa Stata, R, SAS ja MPlus mahdollistavat kaikkien erilaisten monitasomallien rakentamisen. Erityisesti monitasomalleihin erikoistuneita ohjelmia ovat muun muassa MLwiN ja HLM (ks. tilasto-ohjelmia käsittelevä luku).