Logistinen regressio
Markus Kaakinen & Noora Ellonen (Viittausohje. Tämä on uudistettu versio Mikko Mattilan [2003] artikkelista Logistinen regressio)
Tämä on viides osa regressioanalyysista kertovassa luvusta ja pääset alla olevasta listasta siirtymään suoraan muihin luvun osiin.
Logistinen regressioanalyysi on tavanomaisen regressioanalyysin erityistyyppi. Sitä käytetään silloin, kun selitettävä muuttuja voi saada vain kaksi arvoa. Voidaan esimerkiksi pyrkiä selittämään sitä, miten eri tekijät vaikuttavat siihen, onko vastaaja naimisissa vai ei.
Tavallisessa regressioanalyysissa selitettävän muuttujan tulee mieluiten vaihdella laajalla vaihteluvälillä. Regressioanalyysi ei kuitenkaan ole käyttökelpoinen silloin, kun selitettävän muuttujan arvot rajoittuvat vain kahteen vaihtoehtoon. Logistinen regressioanalyysi ei pyri ennustamaan määriä, vaan todennäköisyyksiä. Kyse on siis siitä, millä todennäköisyydellä tarkasteltavana oleva asia tapahtuu tai pätee. Tulokset kertovat, ovatko selittävät muuttujat yhteydessä tapahtuman todennäköisyyteen ja kuinka vahva mahdollinen yhteys on. Esimerkiksi äänestämistutkimuksen tulokset voivat kertoa, että naisilla on suurempi todennäköisyys äänestää kuin miehillä tai että iän kasvaessa osallistumistodennäköisyys kasvaa.
Logistisen regressiomallin idea

Logistisessa regressioanalyysissa selitettävä muuttuja täytyy koodata niin, että se voi saada ainoastaan arvon yksi tai nolla. Oletetaan, että tutkimuksessa on tarkoitus selvittää, mitkä tekijät ovat yhteydessä ihmisten äänestysaktiivisuuteen. Selitettävä muuttuja mittaa sitä, äänestikö vastaaja viime vaaleissa. Se saa arvon nolla, jos vastaaja ei äänestänyt (eli Y=0) ja arvon yksi jos hän äänesti (Y=1).
Logistisen regressioanalyysin ymmärtämiseksi täytyy tietää, mitä vedolla (odds) tarkoitetaan. Oletetaan, että äänestystutkimuksen otoksessa naisista 70 % ja miehistä 60 % ilmoitti äänestäneensä viime vaaleissa. Näiden lukujen avulla voidaan naisille ja miehille laskea äänestämisen veto. Vetolukuja käytetään yleisesti esimerkiksi kuvattaessa vedonlyönnin voittosuhteita. Veto saadaan suhteuttamalla tapahtuman todennäköisyys siihen todennäköisyyteen, että se ei tapahdu. Esimerkiksi yksittäisen naisen kohdalla äänestämisen todennäköisyys on 0,70 ja vastaavasti todennäköisyys, että hän ei käy äänestämässä on 0,3 (=1-0,7). Näin naisten veto on 0,7/0,3=2,33. Vastaavasti miesten veto on 1,5 (=0,6/0,4).
Vetokertoimien avulla voidaan laskea sukupuolen vetosuhde (engl. odds ratio), joka siis viittaa kahden vedon väliseen suhteeseen. Vetosuhde kertoo sen, miten ennustettavan tapahtuman (esimerkiksi äänestämisen) veto muuttuu, kun selittävien muuttujien arvot vaihtelevat. Sukupuolen vetosuhde saataisiin jakamalla naisten veto miesten vedolla (2,33/1,5=1,55). Vetosuhdekerrointa tulkitaan niin, että naisten kohdalla äänestämisen veto on 1,55-kertainen miehiin nähden. Yhtä suuremmat vetosuhteet kertovat, että (mallinnettavan ilmiön) veto kasvaa, kun selittävä muuttuja kasvaa yhdellä yksiköllä. Yhtä pienempi vetosuhde taas viittaa siihen, että selittävän muuttujan kasvaminen pienentää vetoa (arvo 1 tarkoittaa, ettei vedossa ole eroa). Lisäksi on tärkeä huomata, ettei vetosuhde kerro suoraan todennäköisyyksien suhteesta vaan nimenomaan vetojen suhteesta. Kuten esimerkissä yllä todettiin, naisten todennäköisyys äänestää oli 70 % ja miesten 60 %. Todennäköisyys on siis noin 1,2-kertainen. Yhtä isompi vetosuhde kuitenkin tarkoittaa, että myös tapahtuman todennäköisyys kasvaa (jossain määrin). Yhtä pienempi kerroin taas tarkoittaa, että todennäköisyys pienenee.
Veto ja vetosuhde voivat saada arvoja nollan ja äärettömän välillä. Tavanomainen regressioanalyysi soveltuu kuitenkin parhaiten tilanteeseen, missä selitettävän muuttujan arvoja ei ole rajattu millekään ennalta määrätylle välille. Siksi logistista regressioanalyysia varten vedosta otetaan vielä luonnollinen logaritmi. Tämä varmistaa sen, että saatu luku vaihtelee äärettömän pienien ja äärettömän suurien lukujen välillä.
Yksinkertaistettuna logistinen regressiomalli on tavallinen regressiomalli, jossa selitettävänä muuttujana on tutkittavan tapahtuman vedon logaritmi. Tämä voidaan ilmaista kaavalla seuraavasti:
Kaavassa P(Y=1) \( P(Y=1) \) on todennäköisyys sille, että selitettävä muuttuja saa arvon yksi, a \( a \) on vakiotekijä, b \( b \) regressiokerroin ja x \( x \) selittävän muuttujan arvo. Logistisen regressiomallin kaavan lauseke a + bx \( a + bx \) on täsmälleen sama kuin lineaarisessa regressioanalyysissä. Siksi logistisen regressiomallin tulkinta ja siihen liittyvät ongelmat ovat lähes samat kuin regressioanalyysissa.
Tulkinnassa täytyy kuitenkin ottaa huomioon se, että logistisessa regressiomallissa selittävien muuttujien ja selitettävän vedon yhteys ei ole lineaarinen. Yhteyden oletetaan seuraavan niin sanotun s -käyrän (eli logistisen käyrän) muotoa. S-käyrässä selittävät muuttujat ovat heikommin yhteydessä todennäköisyyteen jakauman ääripäissä. Tämä on yleensä uskottava oletus dikotomisen vastemuuttujan ja selittävien muuttujien välisestä suhteesta. Logistinen yhteys voidaan ymmärtää myös niin, että mallissa selittävät muuttujat ovat lineaarisesti yhteydessä mallinnettavan vedon logistiseen muunnokseen. Kuviossa 1 on esitetty kuvitteellinen esimerkki logistisista käyristä. Esimerkissä selittävä muuttuja x -akselilla saa arvoja nollasta kymmeneen. Logistisen regressioanalyysin tulos on y -akselilla. Logistisessa regressioanalyysissa selitettävän tapahtuman todennäköisyys saa arvoja nollan ja yhden välillä.
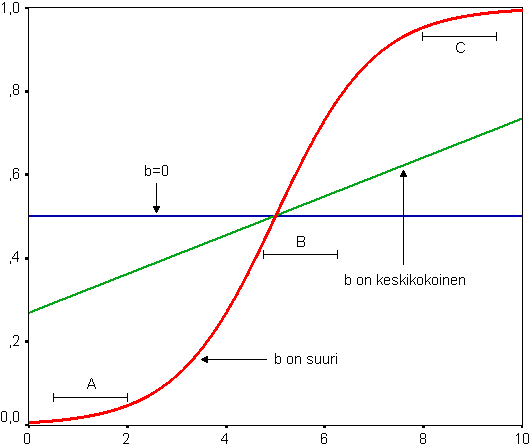
Vetosuhteiden lisäksi logistisen regressioanalyysin tulokset esitetään usein regressiokertoimien avulla. Regressiokertoimet ovat siis yllä olevan kaavan mukaisesti yhtä kuin vetosuhteen logaritmi. Näin laskettuja regressiokertoimia tulkitaan samoin kuin lineaarisen regression kertoimia. Jos selittävällä ja selitettävällä muuttujalla ei ole lainkaan yhteyttä toisiinsa logistisessa regressiomallissa, saa regressiokerroin b itseisarvoltaan hyvin pienen arvon. Kuten kuviosta 1 nähdään, on muuttujien yhteyttä kuvaava käyrä täysin vaakasuora silloin, kun b saa arvon nolla. Tämä osoittaa sen, että selitettävän muuttujan mittaaman tapahtuman todennäköisyys ei muutu ollenkaan selittävän muuttujan arvojen vaihdellessa.
Silloin kun kerroin b saa suuren arvon, on selittävän muuttujan arvojen ja tapahtuman todennäköisyyden yhteyttä kuvaava käyrä s-kirjaimen muotoinen. Tämä tarkoittaa sitä, että jos selittävän muuttujan pieni arvo kasvaa hiukan, ei tämä muuta paljoakaan selitettävän muuttujan mittaaman tapahtuman todennäköisyyttä (väli A). Sen sijaan selittävän muuttujan saadessa arvoja vaihteluvälin keskivaiheilta pienikin muutos aiheuttaa suuren muutoksen selitettävän ilmiön tapahtumistodennäköisyydessä (väli B). Selittävän muuttujan ollessa lähellä ylärajaa muutoksilla on jälleen pienempi vaikutus (väli C).
Kun kertoimen b arvo on keskikokoinen, on sen muoto vaakasuoran ja s -käyrän välimailla. Jos kertoimen arvo on negatiivinen, laskee selitettävän muuttujan mittaaman tapahtuman todennäköisyys selittävän muuttujan arvon kasvaessa. Tällöin logistiset käyrät ovat samanmuotoisia kuin kuviossa 1, mutta ne laskevat vasemmalta oikealle.
Logistisen regressiomallin kertoimien tulkinta eroaa tavallisen regressiomallin kertoimien tulkinnasta siinä, että tavallisessa regressiomallissa yhden yksikön muutos selittävässä muuttujassa aiheuttaa aina samansuuruisen muutoksien selitettävässä muuttujassa. Sen sijaan logistisessa regressioanalyysissa selitettävän todennäköisyyden muutos riippuu b -kertoimen lisäksi selittävän muuttujan arvosta. Tämän takia logistisen regressiomallin tulosten tulkinta on aina hankalampaa kuin tavallisessa regressiomallissa (Mood 2010).
Logistisen regressiomallin arviointi ja tulkinta

Kuten lineaaristen mallien, myös logistisen regression kohdalla tulosten luotettavuus perustuu tiettyihin oletuksiin. Logistinen regressiomalli olettaa ensinnäkin mallinnettavan todennäköisyyden ja selittävien muuttujien välisen yhteyden olevan logistinen (ei siis lineaarinen). Myös logistisessa regressiossa mallin tulee sisältää kaikki olennaiset muuttujat (ks. Regressioanalyysin oletukset, Oletus 5). Lineaaristen mallien tavoin myös logistinen regressioanalyysi olettaa, etteivät selittävien muuttujien välillä ole (täydellistä) multikollineaarisuutta (Oletus 3) ja että havainnot ovat toisistaan riippumattomia (Oletus 7).
Logististen ja lineaaristen mallien tulkinnan välillä on myös muita eroja, jotka tulee ottaa huomioon tulosten tulkinnassa (ks. esim. Mood, 2010). Logistisessa regressiossa mallien kertoimiin vaikuttavat myös sellaiset muuttujat, jotka ovat yhteydessä mallinnettuun todennäköisyyteen, mutta eivät ole mukana mallissa. Toisin sanoen mallin selitysaste vaikuttaa havaittujen kertoimien skaalaan. Mitä enemmän mallissa on mukana selitysvoimaisia muuttujia, sen suurempi on kertoimien skaala.
Näin ollen logististen mallien regressiokertoimet tai vetosuhteet eivät ole yhteismitallisia yhteyden voimakkuuden indikaattoreita tai suoraan verrannollisia eri otosten tai mallien välillä. Ongelma voidaan ottaa osin huomioon esimerkiksi raportoimalla regressiokertoimien ja vetosuhteen lisäksi niin sanotut marginaaliefekti-kertoimet (AME) tai käyttää logistisen mallin sijaan niin sanottua lineaarista todennäköisyysmallinnusta (engl. linear probability modelling) (Mood 2010).
Esimerkki logistisesta regressioanalyysista

Logistisen regressioanalyysin esimerkissä tutkitaan, mitkä tekijät vaikuttavat talouskasvun asettamiseen ympäristönsuojelun edelle. Vuoden 2017 European Values Study Suomen osa-aineistossa (ks. aineistokuvaus). on kysymys, jossa vastaajien piti valita kahdesta asenneväittämävaihtoehdosta, kumpi on heidän mielestään parempi (q57). Nämä vaihtoehdot olivat 1. Ympäristön suojeleminen tulisi asettaa etusijalle, vaikka se hidastaakin talouskasvua ja vie joitakin työpaikkoja ja 2.Talouskasvu ja työpaikkojen luominen pitäisi asettaa etusijalle, vaikka ympäristö kärsiikin siitä jossain määrin. Näistä jälkimmäinen edustaa talouskasvua suosivaa ajattelutapaa.
Vastaajista 86 % valitsi jommankumman näistä vaihtoehdoista ja 14 % vastasi jotain muuta tai ei halunnut valita näiden väliltä. Analyysia varten muuttuja on koodattu niin, että ensimmäinen vaihtoehto saa arvon nolla ja jälkimmäinen arvon yksi. Näin logistisen regressioanalyysin avulla voidaan tutkia siis, mitkä tekijät ovat yhteydessä vastaajien todennäköisyyteen valita talouskasvua suosiva vaihtoehto.
Analyysin selittäjinä käytetään viittä eri muuttujaa. Demografisista muuttujista mukana ovat vastaajan ikä ja sukupuoli (mies=0, nainen=1). Vastaajan tulotasoa mitataan 10-luokkaisella muuttujalla, jossa suuret arvot tarkoittavat korkeampia tuloja. Analyyseissä tätä muuttujaa kohdellaan jatkuvana muuttujana. Asennemuuttujista mukana on vastaajien suhtautuminen ympäristönsuojeluun. Tämä on summamuuttuja kahdesta asennemuuttujasta, ja sen saamat matalat arvot kertovat kielteisestä ja korkeammat arvot positiivisesta suhtautumisesta ympäristönsuojeluun. Lisäksi mallissa on mukana muuttuja, joka kuvaa vastaajan sijoittumista politiikan vasemmisto-oikeisto -ulottuvuudella. Se saa arvoja yhdestä kymmeneen pienten arvojen kuvastaessa sijoittumista vasemmalle.
| B | Keskivirhe | p-arvo | Exp(B) | 95 % luottamusväli | ||
| Sukupuoli | 0,04 | 0,18 | 0,815 | 1,04 | 0,74 | 1,48 |
| Ikä | 0,00 | 0,01 | 0,899 | 1,00 | 0,99 | 1,01 |
| Tulotaso | -0,00 | 0,03 | 0,930 | 1,00 | 0,93 | 1,07 |
| Sijoittuminen vasemmisto–oikeisto-jatkumolla | 0,20 | 0,04 | <0,001 | 1,22 | 1,12 | 1,32 |
| Suhtautuminen ympäristönsuojeluun | -1,75 | 0,15 | <0,001 | 0,17 | 0,13 | 0,23 |
| Vakio | 3,66 | 0,65 | <0,001 | 38,75 | ||
Logistisen regressioanalyysin tulokset ovat taulukossa 1. Mallin tarkastelu kannattaa aloittaa muuttujien merkitsevyystasojen analyysilla. Selittävistä muuttujista sijoittuminen vasemmisto–oikeisto-jatkumolla (p < 0,001) ja suhtautuminen ympäristönsuojeluun (p < 0,001) ovat tilastollisesti erittäin merkitsevästi yhteydessä talouskasvua suosiviin asenteisiin. Mitä enemmän vastaaja sijoittaa itsensä oikealle vasemmisto–oikeisto-jatkumolla, sen todennäköisemmin hän suosii talouskasvua (B = 0,20). Mallin vetosuhteen (Exp(B)) perusteella voidaan sanoa, että kun vasemmisto–oikeisto-muuttuja kasvaa yhdellä yksiköllä, talouskasvun suosimisen veto kasvaa 1,22-kertaiseksi. Mitä positiivisemmin vastaaja suhteutuu ympäristön suojeluun, sitä epätodennäköisemmin hän valitsee talouskasvua suosivan vaihtoehdon (B = -1,75).
Logistisen regressiomallin ennustearvoa voidaan tarkastella katsomalla, kuinka hyvin sen avulla pystytään luokittelemaan vastaajat oikeisiin luokkiin heidän vastaustensa mukaan. Taulukon 1 regressiomalli ennustaa oikein 94 prosenttia niistä vastaajista, jotka valitsivat ympäristönsuojelun. Toisaalta malli ennustaa oikein vain 39 prosenttia niistä, jotka valitsivat talouskasvua arvostavan vaihtoehdon (Regressioanalyysin yksityiskohtaista SPSS-tulostaulua voit tarkastella harjoituksessa 3). Kaiken kaikkiaan malli osuu siis oikeaan 81 prosentissa kaikista tapauksista ja erehtyy n. joka viidennen havainnon kohdalla. Näin mallin ennustekyky on parhaimmillaankin vain kohtalainen. Toisin sanoen taulukon 1 sisältämien muuttujien avulla ei pystytä ennustamaan kovinkaan tarkasti vastaajien kantaa talouskasvun suosimiseen.
Mallin selityskykyä arvioidaan myös usein niin sanotun pseudo-R2-kertoimen avulla (esim. McFadden R2 tai Cox and Snell R2). Myös sen laskeminen perustuu yllä kuvattuihin ennustettuihin todennäköisyyksiin ja vastemuuttujan havaittuihin arvoihin. Näitä kertoimia tulkitaan kuten lineaarisen regressioanalyysin R2-kertoimia. Ne saavat arvoja nollan ja yhden välillä. Lähellä yhtä olevat arvot kertovat erittäin hyvästä selitysasteesta. Lähellä nollaa olevat arvot taas viittaavat siihen, ettei malli ennusta selitettävän muuttujan vaihtelua.
On huomattava, että selitettävänä muuttujana ollut talouskasvu on hyvin karkea, ja suhtautumista olisikin kannattanut mitata laajemmalla skaalalla. Logistista regressioanalyysia onkin tarkoituksenmukaisinta käyttää silloin, kun selitettävää ilmiötä ei ole mitattu tai ei voida mitata tarkemmin kuin kaksijakoisesti.
Multinomiaalinen logistinen regressio

Multinomiaalinen logistinen regressio (multinomial logistic regression) on tavallisen logistisen regressioanalyysin laajennus, jossa selitettävä muuttuja voi saada useampia kuin pelkästään kaksi vaihtoehtoa. Kuvitellaan esimerkiksi tilanne, jossa luokitteluasteikolla mitattu selitettävä muuttuja voi saada kolme eri vaihtoehtoa: A, B ja C. Multinomiaalisessa logistisessa regressioanalyysissa tutkitaan, mitkä tekijät ovat yhteydessä siihen, että vastaaja on valinnut tietyn vaihtoehdon suhteessa valittuun referenssivaihtoehtoon. Oletetaan edelleen, että esimerkkianalyysissa referenssivaihtoehtona on A. Analyysin tarkoitus on siis selvittää, mitkä tekijät ennustavat sitä, että vastaaja on valinnut A:n sijaan vaihtoedon B tai C. Käytännössä tämä tarkoittaa sitä, että esimerkkianalyysin tuloksena saadaan kaksi erilaista mallia. Ensimmäisessä mallissa verrataan vaihtoehdon B valintaa suhteessa vaihtoehtoon A ja toisessa vaihtoehto C:n valintaa suhteessa A:han.
Tässä yhteydessä ei käsitellä multinomiaalista logistista regressioanalyysia tarkemmin. Menetelmästä kiinnostuneen kannattaa katsoa alta kirjallisuusvinkkejä.