Mittaaminen: Tilastoyksikkö, muuttujat ja havaintomatriisi

Tämä luku jakautuu neljään osaan. Pääset liikkumaan osien välillä alla olevasta listasta.

Yhteiskuntatieteissä tiedonkeruun kohteena ovat usein yksittäiset ihmiset. Tällöin mittauksen kohteena olevat henkilöt ovat kvantitatiivisen tutkimuksen käsitteillä ilmaistuna tilastoyksikköjä tai havaintoyksikköjä. Tilastoyksikkö voi myös olla jokin muu konkreettinen tai abstrakti kohde.

Ihmisillä on tilastoyksikköinä erilaisia tutkimuksellisia rooleja: asiakas, osallistuja, matkustaja, äänestäjä, kuluttaja, työtön, vanhus, potilas, tiettyyn uskonnolliseen yhteisöön kuuluva, opiskelija, asiantuntija, ruotsinsuomalainen tai saamelainen. Tilastoyksikkö voi olla myös organisaatio tai yhteisö: valtio, kansa, perhe, koulu, yritys, yliopisto, sairaala. Sanomalehti tai siinä oleva uutinen voi olla perusyksikkö, josta kerätään tietoa. Toisaalta tilastoyksikkö voi olla abstrakti, kuten asiakassuhde. Tällöin konkreettinen tieto voidaan kerätä useista lähteistä: asiakassuhteessa olevilta henkilöiltä, tilannehavainnointina, rekistereistä ja asiapapereista. Yksittäiset asiakirjat, esimerkiksi perukirja tai mielentilalausunto, voivat myös olla tutkimuksen kohteina tai tutkimuskohteen edustajina.

Tarkoituksenmukaisen tilastoyksikön valitseminen ei ole aina yksinkertaista. Mielentilalausuntoja tutkittaessa tilastoyksikkönä voi olla yhtäältä itse lausunto tai toisaalta henkilö, jota se koskee. Tilastoyksikön tarkempi, sisällöllinen määritteleminen voi olla vaikeaa, kun tilastoyksikkönä on esimerkiksi perhe. Tutkimuksessa on lähdettävä perhekäsitteen määrittelemisestä kyseisessä tutkimuksessa ja kenties mietittävä muita mahdollisia tilastoyksikkövaihtoehtoja; voisiko yksittäinen perheenjäsen edustaa perhettä tutkimuksen tilastoyksikkönä? Joskus tutkimusta palvelevien johtopäätösten saamiseksi voidaan yhdessä tutkimuksessa tarkastella rinnakkain erilaisia tilastoyksikkövaihtoehtoja, esimerkiksi perheenjäsen ja perhe.

Tutkimuksessa populaatio eli perusjoukko on kohdejoukko, josta tutkimuksessa halutaan tehdä päätelmiä. Joskus on mahdollista tehdä kokonaistutkimus, jossa kerätään tietoja kaikista perusjoukkoon kuuluvista tilastoyksiköistä. Otantatutkimuksessa perusjoukkoa edustaa otos, josta saatuja tuloksia voidaan yleistää perusjoukkoon. Joskus on tarkoituksenmukaisempaa kerätä ns. näyte, joka ei edusta kattavasti perusjoukkoa, mutta jonka avulla saadaan käytössä olevilla resursseilla tarkoituksenmukaisemmin tietoa tutkittavasta asiasta.

Tutkimusta varten tieto on saatettava sellaiseen muotoon, että sitä voidaan johdonmukaisesti ja jäsennellysti käsitellä. Kvantitatiivisessa tutkimuksessa tämä tapahtuu tilastollisten muuttujien avulla. Kun esimerkiksi ihmisiltä kysytään jotakin asiaa, kysymykseen annetut vastaukset eroavat. Yleisesti ottaen tilastoyksiköiden tiedot eroavat toisistaan riippumatta siitä, millä tiedonkeruumenetelmällä ne on tuotettu tai minkä tyyppistä ilmiöaluetta mitataan. Tällaisesta tilastoyksiköihin liittyvästä asiasta tai ominaisuudesta voidaan luoda tilastollinen muuttuja. Muuttujia voivat olla esimerkiksi sukupuoli, ikä tai mielipide, kun tilastoyksikkönä on henkilö. Yrityksen ollessa tilastoyksikkönä muuttujia voivat olla liikevaihto tai henkilöstön määrä. Silloin, kun tietoa kerätään kunnista, muuttujina voivat olla esimerkiksi asukasluku, kuntamuoto tai henkirikosten määrä. Termi 'tilastollinen' korostaa sitä, että mittauksessa saatu muuttujan arvo on tietyllä hetkellä tilastoitu tieto, useimmiten luku, joka tiivistää mahdollisesti hyvinkin moniulotteisen ominaisuuden.

Kyselytutkimuksessa tilastollinen muuttuja voidaan muodostaa kysymyksestä tai väittämästä. Tavallisesti vastauksista saadaan muuttujan arvoiksi numeroita. Kysymyksiin annetut vastaukset ovat muuttujan arvoja. Jos tutkittaisiin täysi-ikäisiä työelämässä olevia henkilöitä, ikämuuttujan mahdolliset arvot olisivat välillä 18 - 65 vuotta. Kun tietyn henkilön ikä on 50 vuotta, tämä voidaan ilmaista tilastotieteen kielellä seuraavasti: tilastoyksikön a _i saama muuttujan x arvo on 50 vuotta. Sukupuolimuuttujan mahdolliset arvot ovat 'nainen' ja 'mies'. Tällaiset sanalliset vaihtoehdot käsitellään tilasto-ohjelmilla yleensä numeroiksi muutettuina, jolloin kutakin vaihtoehtoa vastaa yksikäsitteinen numeerinen koodi. Esimerkiksi sukupuoli voidaan koodata siten, että numero 1 tarkoittaa naista ja numero 2 miestä.

Tutkimuksen näkökulmasta muuttujat voidaan jaotella mm. taustamuuttujiin ja varsinaisiin tutkimusmuuttujiin. Tutkimusmuuttujat liittyvät välittömästi tutkittavaan ilmiöön; sen sijaan taustamuuttujat antavat yleisempää tietoa tilastoyksiköstä. Käytännössä jako ei ole välttämättä täysin yksiselitteinen. Eniten käytettyjä taustamuuttujia ovat sukupuoli, siviilisääty, syntymävuosi, ikä ja koulutus. Joskus taustamuuttujiksi voidaan lukea hiukan erityisempiäkin muuttujia. Esimerkiksi Tilastokeskuksen vaalimenestysanalyysissä 2003 (Avautuu uuteen välilehteen) taustamuuttujina käytettiin alueittaisista muuttujista mm. työllisyyttä, elinkeinorakennetta, kaupungistumisastetta, eläkeläisten osuutta ja puolueiden kannatuspohjaa (KESK - KOK - SDP - VAS). Työterveyslaitoksen lääkärien työoloja ja kuormittuneisuutta selvittävässä tutkimuksessa taustamuuttujiksi nimettiin tyypillisten sukupuolen ja iän lisäksi päätoimipaikka, nimike päätoimessa, työsuhteen vakinaisuus sekä erikoistuminen. Varsinaisia tutkimusmuuttujia olivat mm. työaika, työtahdin kokeminen ja työtahdin kiristymisen syyt. (Töyry ym. 1999).

Muuttujia voidaan jaotella myös sillä perusteella, kuinka välittömästi ne mittaavat tutkittavia asioita. Useat henkilöitä koskevat taustatiedot lukeutuvat muuttujiin, joilla on tarkoitus mitata vain ja ainoastaan kysymyksessä mainittua asiaa, esim. sukupuoli. Kun taas kysytään "Oletko puolueen jäsen?" ei välttämättä ollakaan kiinnostuneita pelkästään puolueen jäsenyydestä, vaan kysymyksen tarkoituksena voi olla selvittää henkilön poliittista aktiivisuutta. Tällöin puolueen jäsenyys indikoi poliittista aktiivisuutta ja siitä voidaan käyttää nimitystä indikaattorimuuttuja. Myös syntymävuosi voidaan ymmärtää indikaattorimuuttujaksi. On eri asia olla kiinnostunut syntymävuodesta, johon liittyy erilaisia historiallisia tapahtumia, kuin olla kiinnostunut vain henkilön iästä. Myös kysymyspatteristot koostuvat usein indikaattorimuuttujista, joilla operationalisoidaan erilaisia käsitteitä.

Havaintomatriisi

Tilastoyksikköjä koskevat tiedot on koottava järkevään muotoon aineiston käsittelyä varten. Yleensä havainnot tallennetaan tilasto-ohjelmissa matriisiksi. Sen kullakin vaakarivillä on yhden tilastoyksikön saamat muuttujien arvot. Tietyn muuttujan arvot puolestaan sijaitsevat samoissa sarakkeissa kaikilla tilastoyksiköillä. Kuvion 1 havaintomatriisissa on sukupuolta ja ikää koskevat tiedot seitsemältä henkilöltä. Lisäksi ensimmäisessä sarakkeessa on vastauslomakkeen numero. Tilasto-ohjelmistot käyttävät havaintomatriisia perusdatana, josta ne laskevat mm. tunnuslukuja ja piirtävät graafisia esityksiä.

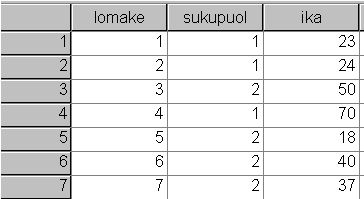
Tilastotieteen kaavoissa tilastoyksiköitä merkitään yleensä kirjaimella a, johon liitetään alaindeksi, esim. a₃. Alaindeksi kertoo, millä rivillä kyseisen tilastoyksikön tiedot ovat. Esimerkiksi yleisempi merkintä a_i, i=1,...,7 tarkoittaa, että aineistossa on seitsemän havaintoyksikköä: a₁, a₂, a₃, a₄, a₅, a₆, a₇.

Formaalisissa matemaattisissa esityksissä, kuten kaavoissa, muuttujien merkitsemiseen käytetään kirjaimia x, y ja z sekä samoja kirjaimia alaindeksillä varustettuina, esim. x₁, x₂, x₃, ... tai yleisesti x_i tai x_j. Viiva kirjaimen alla viittaa siihen, että muuttujan arvo vaihtelee satunnaisesti, tiettyjen sallittujen arvojen puitteissa. Kun viiva jätetään pois, merkintä tarkoittaa satunnaismuuttujan saamaa numeerista arvoa; voidaan siis kirjoittaa x₃ = x, jossa x on yleisesti jokin muuttujan x₃ numeerinen arvo. Esimerkiksi merkintä x_i, i = 1, 2, 3 ... 20 tarkoittaa, että muuttuja vaihtuu, kun alaindeksi vaihtuu.

Havaintomatriisi voidaan kirjoittaa yleisessä muodossa käyttämällä kirjaimia. Kirjain n on tilastoyksiköiden määrä aineistossa ja kirjain k muuttujien määrä. Merkintä x_ij tarkoittaa solussa ij olevaa muuttujan arvoa.

Taulukko 1. Esimerkki havaintomatriisista.

	x 1	x 2	...	...	x k-1	x k
a 1	x 11	x 12	...	...	x 1,k-1	...
a 2	x 21	x 22	...	...	x 2,k-1	...
...	...	...	...	...	...	...
...	...	...	...	...	...	...
a n-1	x n-1,1	x n-1,2	...	...	x n-1,k-1	x n-1,k
a n	x n,1	x n,2	...	...	x n,k-1	x n,k

Harjoitus

Tehtävä 1. Määrittele tilastoyksikkö, perusjoukko ja tilastolliset muuttujat tutkittaessa

1. Suomen väestön ikärakennetta
2. vallitseeko sukupuolen ja alkoholin käytön välillä riippuvuutta
3. koulussa menestymisen ja sosiaaliryhmän välistä riippuvuutta
4. miten kunnan työttömyysaste vaikuttaa rikollisuuteen